The theory of supercompensation: Strength training frequency and muscle gain

Moderate strength training has a number of health benefits, and is viewed by many as an important component of a natural lifestyle that approximates that of our Stone Age ancestors. It increases bone density, muscle mass, and improves a number of health markers. Done properly, it may decrease body fat percentage.

Generally one would expect some muscle gain as a result of strength training. Men seem to be keen on upper-body gains, while women appear to prefer lower-body gains. Yet, many people do strength training for years, and experience little or no muscle gain.

Paradoxically, those people experience major strength gains, both men and women, especially in the first few months after they start a strength training program. However, those gains are due primarily to neural adaptations, and come without any significant gain in muscle mass. This can be frustrating, especially for men. Most men are after some noticeable muscle gain as a result of strength training. (Whether that is healthy is another story, especially as one gets to extremes.)

After the initial adaptation period, of “beginner” gains, typically no strength gains occur without muscle gains.

The culprits for the lack of anabolic response are often believed to be low levels of circulating testosterone and other hormones that seem to interact with testosterone to promote muscle growth, such as growth hormone. This leads many to resort to anabolic steroids, which are drugs that mimic the effects of androgenic hormones, such as testosterone. These drugs usually increase muscle mass, but have a number of negative short-term and long-term side effects.

There seems to be a better, less harmful, solution to the lack of anabolic response. Through my research on compensatory adaptation I often noticed that, under the right circumstances, people would overcompensate for obstacles posed to them. Strength training is a form of obstacle, which should generate overcompensation under the right circumstances. From a biological perspective, one would expect a similar phenomenon; a natural solution to the lack of anabolic response.

This solution is predicted by a theory that also explains a lack of anabolic response to strength training, and that unfortunately does not get enough attention outside the academic research literature. It is the theory of supercompensation, which is discussed in some detail in several high-quality college textbooks on strength training. (Unlike popular self-help books, these textbooks summarize peer-reviewed academic research, and also provide the references that are summarized.) One example is the excellent book by Zatsiorsky & Kraemer (2006) on the science and practice of strength training.

The figure below, from Zatsiorsky & Kraemer (2006), shows what happens during and after a strength training session. The level of preparedness could be seen as the load in the session, which is proportional to: the number of exercise sets, the weight lifted (or resistance overcame) in each set, and the number of repetitions in each set. The restitution period is essentially the recovery period, which must include plenty of rest and proper nutrition.

Note that toward the end there is a sideways S-like curve with a first stretch above the horizontal line and another below the line. The first stretch is the supercompensation stretch; a window in time (e.g., a 20-hour period). The horizontal line represents the baseline load, which can be seen as the baseline strength of the individual prior to the exercise session. This is where things get tricky. If one exercises again within the supercompensation stretch, strength and muscle gains will likely happen. (Usually noticeable upper-body muscle gain happens in men, because of higher levels of testosterone and of other hormones that seem to interact with testosterone.) Exercising outside the supercompensation time window may lead to no gain, or even to some loss, of both strength and muscle.

Timing strength training sessions correctly can over time lead to significant gains in strength and muscle (see middle graph in the figure below, also from Zatsiorsky & Kraemer, 2006). For that to happen, one has not only to regularly “hit” the supercompensation time window, but also progressively increase load. This must happen for each muscle group. Strength and muscle gains will occur up to a point, a point of saturation, after which no further gains are possible. Men who reach that point will invariably look muscular, in a more or less “natural” way depending on supplements and other factors. Some people seem to gain strength and muscle very easily; they are often called mesomorphs. Others are hard gainers, sometimes referred to as endomorphs (who tend to be fatter) and ectomorphs (who tend to be skinnier).

It is not easy to identify the ideal recovery and supercompensation periods. They vary from person to person. They also vary depending on types of exercise, numbers of sets, and numbers of repetitions. Nutrition also plays a role, and so do rest and stress. From an evolutionary perspective, it would seem to make sense to work all major muscle groups on the same day, and then do the same workout after a certain recovery period. (Our Stone Age ancestors did not do isolation exercises, such as bicep curls.) But this will probably make you look more like a strong hunter-gatherer than a modern bodybuilder.

To identify the supercompensation time window, one could employ a trial-and-error approach, by trying to repeat the same workout after different recovery times. Based on the literature, it would make sense to start at the 48-hour period (one full day of rest between sessions), and then move back and forth from there. A sign that one is hitting the supercompensation time window is becoming a little stronger at each workout, by performing more repetitions with the same weight (e.g., 10, from 8 in the previous session). If that happens, the weight should be incrementally increased in successive sessions. Most studies suggest that the best range for muscle gain is that of 6 to 12 repetitions in each set, but without enough time under tension gains will prove elusive.

The discussion above is not aimed at professional bodybuilders. There are a number of factors that can influence strength and muscle gain other than supercompensation. (Still, supercompensation seems to be a “biggie”.) Things get trickier over time with trained athletes, as returns on effort get progressively smaller. Even natural bodybuilders appear to benefit from different strategies at different levels of proficiency. For example, changing the workouts on a regular basis seems to be a good idea, and there is a science to doing that properly. See the “Interesting links” area of this web site for several more focused resources of strength training.

Reference:

Zatsiorsky, V., & Kraemer, W.J. (2006). Science and practice of strength training. Champaign, IL: Human Kinetics.

Total cholesterol and cardiovascular disease: A U-curve relationship

The hypothesis that blood cholesterol levels are positively correlated with heart disease (the lipid hypothesis) dates back to Rudolph Virchow in the mid-1800s.

One famous study that supported this hypothesis was Ancel Keys's Seven Countries Study, conducted between the 1950s and 1970s. This study eventually served as the foundation on which much of the advice that we receive today from doctors is based, even though several other studies have been published since that provide little support for the lipid hypothesis.

The graph below (from O Primitivo) shows the results of one study, involving many more countries than Key's Seven Countries Study, that actually suggests a NEGATIVE linear correlation between total cholesterol and cardiovascular disease.

Now, most relationships in nature are nonlinear, with quite a few following a pattern that looks like a U-curve (plain or inverted); sometimes called a J-curve pattern. The graph below (also from O Primitivo) shows the U-curve relationship between total cholesterol and mortality, with cardiovascular disease mortality indicated through a dotted red line at the bottom.

This graph has been obtained through a nonlinear analysis, and I think it provides a better picture of the relationship between total cholesterol (TC) and mortality. Based on this graph, the best range of TC that one can be at is somewhere between 210, where cardiovascular disease mortality is minimized; and 220, where total mortality is minimized.

The total mortality curve is the one indicated through the full blue line at the top. In fact, it suggests that mortality increases sharply as TC decreases below 200.

Now, these graphs relate TC with disease and mortality, and say nothing about LDL cholesterol (LDL). In my own experience, and that of many people I know, a TC of about 200 will typically be associated with a slightly elevated LDL (e.g., 110 to 150), even if one has a high HDL cholesterol (i.e., greater than 60).

Yet, most people who have a LDL greater than 100 will be told by their doctors, usually with the best of the intentions, to take statins, so that they can "keep their LDL under control". (LDL levels are usually calculated, not measured directly, which itself creates a whole new set of problems.)

Alas, reducing LDL to 100 or less will typically reduce TC below 200. If we go by the graphs above, especially the one showing the U-curves, these folks' risk for cardiovascular disease and mortality will go up - exactly the opposite effect that they and their doctors expected. And that will cost them financially as well, as statin drugs are expensive, in part to pay for all those TV ads.

What is your optimal weight? Maybe it is the one that minimizes your waist-to-weight ratio

There is a significant amount of empirical evidence suggesting that, for a given individual and under normal circumstances, the optimal weight is the one that maximizes the ratio below, where: L = lean body mass, and T = total mass.

L / T

L is difficult and often costly to measure. T can be measured easily, as one’s total weight.

Through some simple algebraic manipulations, you can see below that the ratio above can be rewritten in terms of one’s body fat mass (F).

L / T = (T – F) / T = 1 – F / T

Therefore, in order to maximize L / T, one should maximize 1 – F / T. This essentially means that one should minimize the second term, or the ratio below, which is one’s body fat mass (F) divided by one’s weight (T).

F / T

So, you may say, all I have to do is to minimize my body fat percentage. The problem with this is that body fat percentage is very difficult to measure with precision, and, perhaps more importantly, body fat percentage is associated with lean body mass (and also weight) in a nonlinear way.

In English, it becomes increasingly difficult to retain lean body mass as one's body fat percentage goes down. Mathematically, body fat percentage (F / T) is a nonlinear function of T, where this function has the shape of a J curve.

This is what complicates matters, making the issue somewhat counterintuitive. Six-pack abs may look good, but many people would have to sacrifice too much lean body mass for their own good to get there. Genetics definitely plays a role here, as well as other factors such as age.

Keep in mind that this (i.e., F / T) is a ratio, not an absolute measure. Given this, and to facilitate measurement, we can replace F with a variable that is highly correlated with it, and that captures one or more important dimensions particularly well. This new variable would be a proxy for F. One the most widely used proxies in this type of context is waist circumference. We’ll refer to it as W.

W may well be a very good proxy, because it is a measure that is particularly sensitive to visceral body fat mass, an important dimension of body fat mass. W likely captures variations in visceral body fat mass at the levels where this type of body fat accumulation seems to cause health problems.

Therefore, the ratio that most of us would probably want to minimize is the following, where W is one’s waist circumference, and T is one’s weight.

W / T = waist / weight

Based on the experience of HCE () users, variations in this ratio are likely to be small and require 4-decimals or more to be captured. If you want to avoid having so many decimals, you can multiply the ratio by 1000. This will have no effect on the use of the ratio to find your optimal weight; it is analogous to multiplying a ratio by 100 to express it as a percentage.

Also based on the experience of HCE users, there are fluctuations that make the ratio look like it is changing direction when it is not actually doing that. Many of these fluctuations may be due to measurement error.

If you are obese, as you lose weight through dieting, the waist / weight ratio should go down, because you will be losing more body fat mass than lean body mass, in proportion to your total body mass.

It would arguably be wise to stop losing weight when the waist / weight ratio starts going up, because at that point you will be losing more lean body mass than body fat mass, in proportion to your total body mass.

One’s lowest waist / weight ratio at a given point in time should vary depending on a number of factors, including: diet, exercise, general lifestyle, and age. This lowest ratio will also be dependent on one’s height and genetic makeup.

Mathematically, this lowest ratio is the ratio at which d(W / T) / dT = 0 and d(d(W / T) / dT) / dT > 0. That is, the first derivative of W / T with respect to T equals zero, and the second derivative is greater than zero.

The lowest waist / weight ratio is unique to each individual, and can go up and down over time (e.g., resistance exercise will push it down). Here I am talking about one's lowest waist / weight ratio at a given point in time, not one's waist / weight ratio at a given point in time.

This optimal waist / weight ratio theory is one of the most compatible with evidence regarding the lowest mortality body mass index (, ). Nevertheless, it is another ratio that gets a lot of attention in the health-related literature. I am talking about the waist / hip ratio (). In this literature, waist circumference is often used alone, not as part of a ratio.

Vitamin D production from UV radiation: The effects of total cholesterol and skin pigmentation

Our body naturally produces as much as 10,000 IU of vitamin D based on a few minutes of sun exposure when the sun is high. Getting that much vitamin D from dietary sources is very difficult, even after “fortification”.

The above refers to pre-sunburn exposure. Sunburn is not associated with increased vitamin D production; it is associated with skin damage and cancer.

Solar ultraviolet (UV) radiation is generally divided into two main types: UVB (wavelength: 280–320 nm) and UVA (320–400 nm). Vitamin D is produced primarily based on UVB radiation. Nevertheless, UVA is much more abundant, amounting to about 90 percent of the sun’s UV radiation.

UVA seems to cause the most skin damage, although there is some debate on this. If this is correct, one would expect skin pigmentation to be our body’s defense primarily against UVA radiation, not UVB radiation. If so, one’s ability to produce vitamin D based on UVB should not go down significantly as one’s skin becomes darker.

Also, vitamin D and cholesterol seem to be closely linked. Some argue that one is produced based on the other; others that they have the same precursor substance(s). Whatever the case may be, if vitamin D and cholesterol are indeed closely linked, one would expect low cholesterol levels to be associated with low vitamin D production based on sunlight.

Bogh et al. (2010) published a very interesting study; one of those studies that remain relevant as time goes by. The link to the study was provided by Ted Hutchinson in the comments sections of a another post on vitamin D. The study was published in a refereed journal with a solid reputation, the Journal of Investigative Dermatology.

The study by Bogh et al. (2010) is particularly interesting because it investigates a few issues on which there is a lot of speculation. Among the issues investigated are the effects of total cholesterol and skin pigmentation on the production of vitamin D from UVB radiation.

The figure below depicts the relationship between total cholesterol and vitamin D production based on UVB radiation. Vitamin D production is referred to as “delta 25(OH)D”. The univariate correlation is a fairly high and significant 0.51.

25(OH)D is the abbreviation for calcidiol, a prehormone that is produced in the liver based on vitamin D3 (cholecalciferol), and then converted in the kidneys into calcitriol, which is usually abbreviated as 1,25-(OH)2D3. The latter is the active form of vitamin D.

The table below shows 9 columns; the most relevant ones are the last pair at the right. They are the delta 25(OH)D levels for individuals with dark and fair skin after exposure to the same amount of UVB radiation. The difference in vitamin D production between the two groups is statistically indistinguishable from zero.

So there you have it. According to this study, low total cholesterol seems to be associated with impaired ability to produce vitamin D from UVB radiation. And skin pigmentation appears to have little effect on the amount of vitamin D produced.

The study has a few weaknesses, as do almost all studies. For example, if you take a look at the second pair of columns from the right on the table above, you’ll notice that the baseline 25(OH)D is lower for individuals with dark skin. The difference was just short of being significant at the 0.05 level.

What is the problem with that? Well, one of the findings of the study was that lower baseline 25(OH)D levels were significantly associated with higher delta 25(OH)D levels. Still, the baseline difference does not seem to be large enough to fully explain the lack of difference in delta 25(OH)D levels for individuals with dark and fair skin.

A widely cited dermatology researcher, Antony Young, published an invited commentary on this study in the same journal issue (Young, 2010). The commentary points out some weaknesses in the study, but is generally favorable. The weaknesses include the use of small sub-samples.

References

Bogh, M.K.B., Schmedes, A.V., Philipsen, P.A., Thieden, E., & Wulf, H.C. (2010). Vitamin D production after UVB exposure depends on baseline vitamin D and total cholesterol but not on skin pigmentation. Journal of Investigative Dermatology, 130(2), 546–553.

Young, A.R. (2010). Some light on the photobiology of vitamin D. Journal of Investigative Dermatology, 130(2), 346–348.

Heavy physical activity may significantly reduce heart disease deaths, especially after age 45

The idea that heavy physical activity is a main trigger of heart attacks is widespread. Often endurance running and cardio-type activities are singled out. Some people refer to this as “death by running”. Others think that strength training has a higher lethal potential. We know based on the Oregon Sudden Unexpected Death Study that this is a myth ().

Here is some evidence that heavy physical activity in fact has a significant protective effect. The graph below shows the number of deaths from coronary heart disease, organized by age group, in longshoremen (dock workers). The shaded bars represent those whose level of activity at work was considered heavy. The unshaded bars represent those whose level of activity at work was considered moderate or light (essentially below the “heavy” level).

The data is based on an old and classic study of 6351 men, aged 35 to 74 years, who were followed either for 22 years, or to death, or to the age of 75. It shows a significant protective effect of heavy activity, especially after age 45 () . The numbers atop the unshaded bars reflect the relative risk of death from coronary heart disease in each age group. For example, in the age group 65-74, the risk among those not in the heavy activity group is 110 percent higher (2.1 times higher) than in the heavy activity group.

It should be noted that this is a cumulative effect, of years of heavy activity. Based on the description of the types of activities performed, and the calories spent, I estimate that the heavy activity group performed the equivalent of a few hours of strength training per week, plus a lot of walking and other light physical activities. The authors of the study concluded that “… repeated bursts of high energy output established a plateau of protection against coronary mortality.”

Heavy physical activity may not make you lose much weight, but has the potential to make you live longer.

Insulin responses to foods rich in carbohydrates and protein

Insulin is often presented as a hormone that is at the core of the diseases of civilization, particularly because of the insulin response elicited by foods rich in refined carbohydrates and sugars. What is often not mentioned is that protein also elicits an insulin response and so do foods where carbohydrates are mixed with fat. Sometimes the insulin responses are way more than one would expect based on the macronutrient compositions of the foods.

Holt et al. (1997; full reference at the end of this post) conducted a classic study of insulin responses. This study has been widely cited, and paints an interesting picture of differences in insulin responses to various foods. But you have to be careful where you look. There has been some confusion about the results because of the way they are often reported in places like Wikipedia and on various Internet sites that refer to the study.

The key thing to bear in mind when reviewing this study is that the amounts of food used were designed to have the same calorie content: 1000 kJ or 240 kcal (i.e., 240 calories). This led to wild variations in the size of the portions that are compared and their weight in grams. Also, some of the food portions are probably not what people usually eat in one sitting.

In Holt et al.’s (1997) study the participants were 41 lean and healthy university students. They were fed 1000 kJ (240 kcal) portions of the test foods on separate mornings after a 10-hour fast overnight. Blood insulin levels were measured at different times within a 120-minute period after each meal. An insulin score was then calculated from the area under the insulin response curve for each food; white bread was used as the reference food.

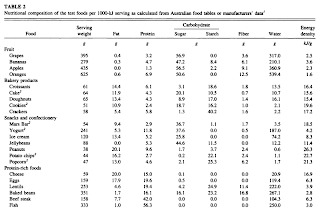
Part of Table 2 on page 1267 is shown below (the full text version of the paper is linked at the end of this post), just to illustrate the types and amounts of food served, and the macronutrient breakdown for each food. I hope you can see what I meant when I said that some of the food portions are probably not what people usually eat in one sitting. I don’t think it would be hard to find someone who would eat 158 g of beef steak in one sitting, but 333 g of fish is a little more difficult. Fish has a higher proportion of protein than beef steak, and thus is more satiating. The same goes for 625 g of orange, about 6 oranges. Foods that have more fat have more calories per gram; hence the smaller portions served for high-fat foods.

Table 4 of the article is a bit long, so I am providing it in two parts below. AUC stands for “area under the curve”. As you can see, for isocaloric portions of different foods (i.e., with the same amount of calories), there is a huge variation in insulin response. The insulin AUCs are shown on the second numeric column from the left. Also note that the insulin responses (AUC) for white bread varied in different meals. This complicates things a bit, but at least provides a more realistic view of the responses since each participant served as his or her own control.

Look at the third column from the right, which shows the insulin responses per gram of each food, compared with the response to white bread, always shown at the top for each group of related foods (e.g., protein-rich foods). The gram-adjusted response for whole-meal bread is rather high, and so is the glucose response. The gram-adjusted insulin response to potatoes is less than one-third of the response to white bread, even though the non-gram-adjusted glucose response is higher. The insulin response to beef is also less than one-third of the response to white bread, gram-for-gram. Even cheese leads to a gram-adjusted response that is about half the one for white bread, and I don’t think many people will eat the same amount of cheese in one sitting as they would do with white bread.

In summary, insulin responses to protein-rich foods are often 50 to 70 percent lower than responses to equivalent amounts of refined carbohydrate-rich foods. Also, insulin responses to unrefined carbohydrate-rich foods (e.g., potato, fruits) are often 70 to 90 percent lower than responses to equivalent amounts of refined carbohydrate-rich foods.

Why do insulin levels go up in response to dietary protein?

One of the reasons is that insulin is needed for tissue protein synthesis. That is, increased circulating protein (as amino acids) and insulin have a net anabolic effect, promoting muscle growth and inhibiting muscle breakdown. (Muscle protein synthesis and breakdown happen all the time; the net effect defines whether muscle grows or shrinks.) In this respect, insulin acts in conjunction with other hormones, such as growth hormone and insulin-like growth factor 1.

Reference:

Holt, S.H., Miller, J.C., & Petocz, P. (1997). An insulin index of foods: The insulin demand generated by 1000-kJ portions of common foods. American Journal of Clinical Nutrition, 66, 1264-1276.