Body fat and disease: How much body fat can I lose in one day?

Body fat is not an inert deposit of energy. It can be seen as a distributed endocrine organ. Body fat cells, or adipocytes, secrete a number of different hormones into the bloodstream. Major hormones secreted by adipose tissue are adiponectin and leptin.

Estrogen is also secreted by body fat, which is one of the reasons why obesity is associated with infertility. (Yes, abnormally high levels of estrogen can reduce fertility in both men and women.) Moreover, body fat secretes tumor necrosis factor, a hormone that is associated with generalized inflammation and a number of diseases, including cancer, when in excess.

The reduction in circulating tumor necrosis factor and other pro-inflammatory hormones as one loses weight is one reason why non-obese people usually experience fewer illness symptoms than those who are obese in any given year, other things being equal. For example, the non-obese will have fewer illness episodes that require full rest during the flu season. In those who are obese, the inflammatory response accompanying an illness (which is necessary for recovery) will often be exaggerated.

The exaggerated inflammatory response to illness often seen in the obese is one indication that obesity in an unnatural state for humans. It is reasonable to assume that it was non-adaptive for our Paleolithic ancestors to be unable to perform daily activities because of an illness. The adaptive response would be physical discomfort, but not to the extent that one would require full rest for a few days to fully recover.

Inflammation markers such as C-reactive protein are positively correlated with body fat. As body fat increases, so does inflammation throughout the body. Lipid metabolism is negatively affected by excessive body fat, and so is glucose metabolism. Obesity is associated with leptin and insulin resistance, which are precursors of diabetes type 2.

Some body fat is necessary for survival; that is normally called essential body fat. The table below (from Wikipedia) shows various levels of body fat, including essential levels. Also shown are body fat levels found in athletes, as well as fit, “not so fit” (indicated as "Acceptable"), and obese individuals. Women normally have higher healthy levels of body fat than men.

If one is obese, losing body fat becomes a very high priority for health reasons.

There are many ways in which body fat can be measured.

When one loses body fat through fasting, the number of adipocytes is not actually reduced. It is the amount of fat stored in adipocytes that is reduced.

How much body fat can a person lose in one day?

Let us consider a man, John, whose weight is 170 lbs (77 kg), and whose body fat percentage is 30 percent. John carries around 51 lbs (23 kg) of body fat. Standing up is, for John, a form of resistance exercise. So is climbing stairs.

During a 24-hour fast, John’s basal metabolic rate is estimated at about 2,550 kcal/day. This is the number of calories John would spend doing nothing the whole day. It can vary a lot for different individuals; here it is calculated as 15 times John’s weight in lbs.

The 2,550 kcal/day is likely an overestimation for John, because the body adjusts its metabolic rate downwards during a fast, leading to fewer calories being burned.

Typically women have lower basal metabolic rates than men of equal weight.

For the sake of discussion, we expect each gram of John’s body fat to contribute about 8 kcals of energy, assuming a rate of conversion of body fat to calories of about 90 percent.

Thus during a 24-hour fast John burns about 318 g of fat, or about 0.7 lbs. In reality, the actual amount may be lower (e.g., 0.35 lbs), because of the body's own down-regulation of its basal metabolic rate during a fast. This down-regulation varies widely across different individuals, and is generally small.

Many people think that this is not much for the effort. The reality is that body fat loss is a long term game, and cannot be achieved through fasting alone; this is a discussion for another post.

It is worth noting that intermittent fasting (e.g., one 24-hour fast per week) has many other health benefits, even if no overall calorie restriction occurs. That is, intermittent fasting is associated with health benefits even if one fasts every other day, and eats twice one's normal intake on the non-fasting days.

Some of the calories being burned during John's 24-hour fast will be from glucose, mostly from John’s glycogen reserves in the liver if he is at rest. Muscle glycogen stores, which store more glucose substrate (i.e., material for production of glucose) than liver glycogen, are mobilized primarily through anaerobic exercise.

Very few muscle-derived calories end up being used through the protein and glycogen breakdown pathways in a 24-hour fast. John’s liver glycogen reserves, plus the body’s own self-regulation, will largely spare muscle tissue.

The idea that one has to eat every few hours to avoid losing muscle tissue is complete nonsense. Muscle buildup and loss happen all the time through amino acid turnover.

Net muscle gain occurs when the balance is tipped in favor of buildup, to which resistance exercise and the right hormonal balance (including elevated levels of insulin) contribute.

One of the best ways to lose muscle tissue is lack of use. If John's arm were immobilized in a cast, he would lose muscle tissue in that arm even if he ate every 30 minutes.

Longer fasts (e.g., lasting multiple days, with only water being consumed) will invariably lead to some (possibly significant) muscle breakdown, as muscle is the main store of glucose-generating substrate in the human body.

In a 24-hour fast (a relatively short fast), the body will adjust its metabolism so that most of its energy needs are met by fat and related byproducts. This includes ketones, which are produced by the liver based on dietary and body fat.

How come some people can easily lose 2 or 3 pounds of weight in one day?

Well, it is not body fat that is being lost, or muscle. It is water, which may account for as much as 75 percent of one’s body weight.

References:

Elliott, W.H., & Elliott, D.C. (2009). Biochemistry and molecular biology. New York: NY: Oxford University Press.

Fleck, S.J., & Kraemer, W.J. (2004). Designing resistance training programs. Champaign, IL: Human Kinetics.

Large, V., Peroni, O., Letexier, D., Ray, H., & Beylot, M. (2004). Metabolism of lipids in human white adipocyte. Diabetes & Metabolism, 30(4), 294-309.

Compensatory adaptation as a unifying concept: Understanding how we respond to diet and lifestyle changes

Trying to understand each body response to each diet and lifestyle change, individually, is certainly a losing battle. It is a bit like the various attempts to classify organisms that occurred prior to solid knowledge about common descent. Darwin’s theory of evolution is a theory of common descent that makes classification of organisms a much easier and logical task.

Compensatory adaptation (CA) is a broad theoretical framework that hopefully can help us better understand responses to diet and lifestyle changes. CA is a very broad idea, and it has applications at many levels. I have discussed CA in the context of human behavior in general (Kock, 2002), and human behavior toward communication technologies (Kock, 2001; 2005; 2007). Full references and links are at the end of this post.

CA is all about time-dependent adaptation in response to stimuli facing an organism. The stimuli may be in the form of obstacles. From a general human behavior perspective, CA seems to be at the source of many success stories. A few are discussed in the Kock (2002) book; the cases of Helen Keller and Stephen Hawking are among them.

People who have to face serious obstacles sometimes develop remarkable adaptations that make them rather unique individuals. Hawking developed remarkable mental visualization abilities, which seem to be related to some of his most important cosmological discoveries. Keller could recognize an approaching person based on floor vibrations, even though she was blind and deaf. Both achieved remarkable professional success, perhaps not as much in spite but because of their disabilities.

From a diet and lifestyle perspective, CA allows us to make one key prediction. The prediction is that compensatory body responses to diet and lifestyle changes will occur, and they will be aimed at maximizing reproductive success, but with a twist – it’s reproductive success in our evolutionary past! We are stuck with those adaptations, even though we live in modern environments that differ in many respects from the environments where our ancestors lived.

Note that what CA generally tries to maximize is reproductive success, not survival success. From an evolutionary perspective, if an organism generates 30 offspring in a lifetime of 2 years, that organism is more successful in terms of spreading its genes than another that generates 5 offspring in a lifetime of 200 years. This is true as long as the offspring survive to reproductive maturity, which is why extended survival is selected for in some species.

We live longer than chimpanzees in part because our ancestors were “good fathers and mothers”, taking care of their children, who were vulnerable. If our ancestors were not as caring or their children not as vulnerable, maybe this blog would have posts on how to control blood glucose levels to live beyond the ripe old age of 50!

The CA prediction related to responses aimed at maximizing reproductive success is a straightforward enough prediction. The difficult part is to understand how CA works in specific contexts (e.g., Paleolithic dieting, low carbohydrate dieting, calorie restriction), and what we can do to take advantage (or work around) CA mechanisms. For that we need a good understanding of evolution, some common sense, and also good empirical research.

One thing we can say with some degree of certainty is that CA leads to short-term and long-term responses, and that those are likely to be different from one another. The reason is that a particular diet and lifestyle change affected the reproductive success of our Paleolithic ancestors in different ways, depending on whether it was a short-term or long-term change. The same is true for CA responses at different stages of one’s life, such as adolescence and middle age; they are also different.

This is the main reason why many diets that work very well in the beginning (e.g., first months) frequently cease to work as well after a while (e.g., a year).

Also, CA leads to psychological responses, which is one of the key reasons why most diets fail. Without a change in mindset, more often than not one tends to return to old habits. Hunger is not only a physiological response; it is also a psychological response, and the psychological part can be a lot stronger than the physiological one.

It is because of CA that a one-month moderately severe calorie restriction period (e.g., 30% below basal metabolic rate) will lead to significant body fat loss, as the body produces hormonal responses to several stimuli (e.g., glycogen depletion) in a compensatory way, but still “assuming” that liberal amounts of food will soon be available. Do that for one year and the body will respond differently, “assuming” that food scarcity is no longer short-term and thus that it requires different, and possibly more drastic, responses.

Among other things, prolonged severe calorie restriction will lead to a significant decrease in metabolism, loss of libido, loss of morale, and physical as well as mental fatigue. It will make the body hold on to its fat reserves a lot more greedily, and induce a number of psychological responses to force us to devour anything in sight. In several people it will induce psychosis. The results of prolonged starvation experiments, such as the Biosphere 2 experiments, are very instructive in this respect.

It is because of CA that resistance exercise leads to muscle gain. Muscle gain is actually a body’s response to reasonable levels of anaerobic exercise. The exercise itself leads to muscle damage, and short-term muscle loss. The gain comes after the exercise, in the following hours and days (and with proper nutrition), as the body tries to repair the muscle damage. Here the body “assumes” that the level of exertion that caused it will continue in the near future.

If you increase the effort (by increasing resistance or repetitions, within a certain range) at each workout session, the body will be constantly adapting, up to a limit. If there is no increase, adaptation will stop; it will even regress if exercise ceases altogether. Do too much resistance training (e.g., multiple workout sessions everyday), and the body will react differently. Among other things, it will create deterrents in the form of pain (through inflammation), physical and mental fatigue, and even psychological aversion to resistance exercise.

CA processes have a powerful effect on one’s body, and even on one’s mind!

References:

Kock, N. (2001). Compensatory Adaptation to a Lean Medium: An Action Research Investigation of Electronic Communication in Process Improvement Groups. IEEE Transactions on Professional Communication, 44(4), 267-285.

Kock, N. (2002). Compensatory Adaptation: Understanding How Obstacles Can Lead to Success. Infinity Publishing, Haverford, PA. (Additional link.)

Kock, N. (2005). Compensatory adaptation to media obstacles: An experimental study of process redesign dyads. Information Resources Management Journal, 18(2), 41-67.

Kock, N. (2007). Media Naturalness and Compensatory Encoding: The Burden of Electronic Media Obstacles is on Senders. Decision Support Systems, 44(1), 175-187.

Large LDL and small HDL particles: The best combination

High-density lipoprotein (HDL) is one of the five main types of lipoproteins found in circulation, together with very low-density lipoprotein (VLDL), intermediate-density lipoprotein (IDL), low-density lipoprotein (LDL), and chylomicrons.

After a fatty meal, the blood is filled with chylomicrons, which carry triglycerides (TGAs). The TGAs are transferred to cells from chylomicrons via the activity of enzymes, in the form of free fatty acids (FFAs), which are used by those cells as sources of energy.

After delivering FFAs to the cells, the chylomicrons progressively lose their TGA content and “shrink”, eventually being absorbed and recycled by the liver. The liver exports part of the TGAs that it gets from chylomicrons back to cells for use as energy as well, now in the form of VLDL. As VLDL particles deliver TGAs to the cells they shrink in size, similarly to chylomicrons. As they shrink, VLDL particles first become IDL and then LDL particles.

The figure below (click on it to enlarge), from Elliott & Elliott (2009; reference at the end of this post), shows, on the same scale: (a) VLDL particles, (b) chylomicrons, (c) LDL particles, and (d) HDL particles. The dark bar at the bottom of each shot is 1000 A in length, or 100 nm (A = angstrom; nm = nanometer; 1 nm = 10 A).

As you can see from the figure, most of the LDL particles shown are about 1/4 of the length of the dark bar in diameter, often slightly more, or about 25-27 nm in size. They come in different sizes, with sizes in this range  being the most common. The smaller and denser they are, the more likely they are to contribute to the formation of atherosclerotic plaque in the presence of other factors, such as chronic inflammation. The larger they become, which usually happens in diets high in saturated fat, the less likely they are to form plaque.

Note that the HDL particles are rather small compared to the LDL particles. Shouldn’t they cause plaque then? Not really. Apparently they have to be small, compared to LDL particles, to do their job effectively.

HDL is a completely different animal from VLDL, IDL and LDL. HDL particles are produced by the liver as dense disk-like particles, known as nascent HDL particles. These nascent HDL particles progressively pick up cholesterol from cells, as well as performing a number of other functions, and “fatten up” with cholesterol in the process.

This process also involves HDL particles picking up cholesterol from plaque in the artery walls, which is one of the reasons why HDL cholesterol is informally called “good” cholesterol. In fact, neither HDL nor LDL are really cholesterol; HDL and LDL are particles that carry cholesterol, protein and fat.

As far as particle size is concerned, LDL and HDL are opposites. Large LDL particles are the least likely to cause plaque formation, because LDL particles have to be approximately 25 nm in diameter or smaller to penetrate the artery walls. With HDL the opposite seems to be true, as HDL particles need to be small (compared with LDL particles) to easily penetrate the artery walls in order to pick up cholesterol, leave the artery walls with their cargo, and have it returned back to the liver.

Another interesting aspect of this cycle is that the return to the liver of cholesterol picked up by HDL appears to be done largely via IDL and LDL particles (Elliott & Elliott, 2009), which get the cholesterol directly from HDL particles! Life is not that simple.

Reference:

William H. Elliott & Daphne C. Elliott (2009). Biochemistry and Molecular Biology. 4th Edition. New York: NY: Oxford University Press.

Sensible sun exposure

Sun exposure leads to the production in the human body of a number of compounds that are believed to be health-promoting. One of these is known as “vitamin D” – an important hormone precursor ().

About 10,000 IU is considered to be a healthy level of vitamin D production per day. This is usually the maximum recommended daily supplementation dose, for those who have low vitamin D levels.

How much sun exposure, when the sun is at its peak (around noon), does it take to reach this level? Approximately 10 minutes.

We produce about 1,000 IU per minute of sun exposure, but seem to be limited to 10,000 IU per day. This assumes a level of skin exposure comparable to that of someone wearing a bathing suit.

Contrary to popular belief, this does not significantly decrease with aging. Among those aged 65 and older, pre-sunburn full-body exposure to sunlight leads to 87 percent of the peak vitamin D production seen in young subjects ().

Evolution seems to have led to a design that favors chronic (every day or so) but relatively brief sun exposure. Most of the sun rays are of the UVA type. However it is the UVB rays, which peak when the sun is high, that stimulate vitamin D production the most. The UVA rays in fact deplete vitamin D. Therefore, after 10 minutes of sun exposure per day when the sun is high, we would be mostly depleting vitamin D by sunbathing when the sun is low.

There is a lot of research that suggests that extended sun exposure also causes skin damage, even exposure below skin cancer levels. Also, anecdotally there are many reports of odd things happening with people who sunbathe for extended periods of time at the pool. Examples are moles appearing in odd places like the bottom of the feet, cases of actinic keratosis, and even temporary partial blindness.

Source: Lifecasting.org

There is something inherently unnatural about sunbathing at the pool, and exponentially more so in tan booths. Hunter-gatherers enjoy much sun exposure by generally avoiding the sun; particularly from the front, as this impairs the vision.

Pools often have reflective surfaces around them, so that people will not burn their feet. They cause glare, and over time likely contribute to the development of cataracts.

When you go to the pool, put your hands perpendicular to your face below you nose so that much of the light coming from those reflective surfaces does not hit your eyes directly. If you do this, you’ll probably notice that the main source of glare is what is coming from below, not from above.

In the African savannas, where our species emerged, this type of reflective surface has no commonly found analog. You don't have to go to the pool to find all kinds of sources of unnatural glare in urban environments.

Snow is comparable. Hunter-gatherers who live in areas permanently or semi-permanently covered with snow, such as the traditional Inuit, have a much higher incidence of cataracts than those who don’t.

So, what would be some of the characteristics of sensible sun exposure during the summer, particular at pools? Considering all that is said above, I’d argue that these should be in the list:

- Standing and moving while sunbathing, as opposed to sitting or lying down.

- Sunbathing for about 10 minutes, when the sun is high, staying mostly in the shade after 10 minutes or so of exposure.

- Wearing eye protection, such as polarized sunglasses.

- Avoiding the sun hitting you directly in the face, even with eye protection, as the facial skin is unlikely to have the same level of resistance to sun damage as other parts that have been more regularly exposed in our evolutionary past (e.g., shoulders).

- Covering those areas that get sunlight perpendicularly while sunbathing when the sun is high, such as the top part of the shoulders if standing in the sun.

Doing these things could potentially maximize the benefits of sun exposure, while at the same time minimizing its possible negative consequences.

The China Study again: A multivariate analysis suggesting that schistosomiasis rules!

In the comments section of Denise Minger’s post on July 16, 2010, which discusses some of the data from the China Study (as a follow up to a previous post on the same topic), Denise herself posted the data she used in her analysis. This data is from the China Study. So I decided to take a look at that data and do a couple of multivariate analyzes with it using WarpPLS (warppls.com).

First I built a model that explores relationships with the goal of testing the assumption that the consumption of animal protein causes colorectal cancer, via an intermediate effect on total cholesterol. I built the model with various hypothesized associations to explore several relationships simultaneously, including some commonsense ones. Including commonsense relationships is usually a good idea in exploratory multivariate analyses.

The model is shown on the graph below, with the results. (Click on it to enlarge. Use the "CRTL" and "+" keys to zoom in, and CRTL" and "-" to zoom out.) The arrows explore causative associations between variables. The variables are shown within ovals. The meaning of each variable is the following: aprotein = animal protein consumption; pprotein = plant protein consumption; cholest = total cholesterol; crcancer = colorectal cancer.

The path coefficients (indicated as beta coefficients) reflect the strength of the relationships; they are a bit like standard univariate (or Pearson) correlation coefficients, except that they take into consideration multivariate relationships (they control for competing effects on each variable). A negative beta means that the relationship is negative; i.e., an increase in a variable is associated with a decrease in the variable that it points to.

The P values indicate the statistical significance of the relationship; a P lower than 0.05 means a significant relationship (95 percent or higher likelihood that the relationship is real). The R-squared values reflect the percentage of explained variance for certain variables; the higher they are, the better the model fit with the data. Ignore the “(R)1i” below the variable names; it simply means that each of the variables is measured through a single indicator (or a single measure; that is, the variables are not latent variables).

I should note that the P values have been calculated using a nonparametric technique, a form of resampling called jackknifing, which does not require the assumption that the data is normally distributed to be met. This is good, because I checked the data, and it does not look like it is normally distributed. So what does the model above tell us? It tells us that:

- As animal protein consumption increases, colorectal cancer decreases, but not in a statistically significant way (beta=-0.13; P=0.11).

- As animal protein consumption increases, plant protein consumption decreases significantly (beta=-0.19; P<0.01). This is to be expected.

- As plant protein consumption increases, colorectal cancer increases significantly (beta=0.30; P=0.03). This is statistically significant because the P is lower than 0.05.

- As animal protein consumption increases, total cholesterol increases significantly (beta=0.20; P<0.01). No surprise here. And, by the way, the total cholesterol levels in this study are quite low; an overall increase in them would probably be healthy.

- As plant protein consumption increases, total cholesterol decreases significantly (beta=-0.23; P=0.02). No surprise here either, because plant protein consumption is negatively associated with animal protein consumption; and the latter tends to increase total cholesterol.

- As total cholesterol increases, colorectal cancer increases significantly (beta=0.45; P<0.01). Big surprise here!

Why the big surprise with the apparently strong relationship between total cholesterol and colorectal cancer? The reason is that it does not make sense, because animal protein consumption seems to increase total cholesterol (which we know it usually does), and yet animal protein consumption seems to decrease colorectal cancer.

When something like this happens in a multivariate analysis, it usually is due to the model not incorporating a variable that has important relationships with the other variables. In other words, the model is incomplete, hence the nonsensical results. As I said before in a previous post, relationships among variables that are implied by coefficients of association must also make sense.

Now, Denise pointed out that the missing variable here possibly is schistosomiasis infection. The dataset that she provided included that variable, even though there were some missing values (about 28 percent of the data for that variable was missing), so I added it to the model in a way that seems to make sense. The new model is shown on the graph below. In the model, schisto = schistosomiasis infection.

So what does this new, and more complete, model tell us? It tells us some of the things that the previous model told us, but a few new things, which make a lot more sense. Note that this model fits the data much better than the previous one, particularly regarding the overall effect on colorectal cancer, which is indicated by the high R-squared value for that variable (R-squared=0.73). Most notably, this new model tells us that:

- As schistosomiasis infection increases, colorectal cancer increases significantly (beta=0.83; P<0.01). This is a MUCH STRONGER relationship than the previous one between total cholesterol and colorectal cancer; even though some data on schistosomiasis infection for a few counties is missing (the relationship might have been even stronger with a complete dataset). And this strong relationship makes sense, because schistosomiasis infection is indeed associated with increased cancer rates. More information on schistosomiasis infections can be found here.

- Schistosomiasis infection has no significant relationship with these variables: animal protein consumption, plant protein consumption, or total cholesterol. This makes sense, as the infection is caused by a worm that is not normally present in plant or animal food, and the infection itself is not specifically associated with abnormalities that would lead one to expect major increases in total cholesterol.

- Animal protein consumption has no significant relationship with colorectal cancer. The beta here is very low, and negative (beta=-0.03).

- Plant protein consumption has no significant relationship with colorectal cancer. The beta for this association is positive and nontrivial (beta=0.15), but the P value is too high (P=0.20) for us to discard chance within the context of this dataset. A more targeted dataset, with data on specific plant foods (e.g., wheat-based foods), could yield different results – maybe more significant associations, maybe less significant.

Below is the plot showing the relationship between schistosomiasis infection and colorectal cancer. The values are standardized, which means that the zero on the horizontal axis is the mean of the schistosomiasis infection numbers in the dataset. The shape of the plot is the same as the one with the unstandardized data. As you can see, the data points are very close to a line, which suggests a very strong linear association.

So, in summary, this multivariate analysis vindicates pretty much everything that Denise said in her July 16, 2010 post. It even supports Denise’s warning about jumping to conclusions too early regarding the possible relationship between wheat consumption and colorectal cancer (previously highlighted by a univariate analysis). Not that those conclusions are wrong; they may well be correct.

This multivariate analysis also supports Dr. Campbell’s assertion about the quality of the China Study data. The data that I analyzed was already grouped by county, so the sample size (65 cases) was not so high as to cast doubt on P values. (Having said that, small samples create problems of their own, such as low statistical power and an increase in the likelihood of error-induced bias.) The results summarized in this post also make sense in light of past empirical research.

It is very good data; data that needs to be properly analyzed!

What is a reasonable vitamin D level?

The figure and table below are from Vieth (1999); one of the most widely cited articles on vitamin D. The figure shows the gradual increase in blood concentrations of 25-Hydroxyvitamin, or 25(OH)D, following the start of daily vitamin D3 supplementation of 10,000 IU/day. The table shows the average levels for people living and/or working in sun-rich environments; vitamin D3 is produced by the skin based on sun exposure.

25(OH)D is also referred to as calcidiol. It is a pre-hormone that is produced by the liver based on vitamin D3. To convert from nmol/L to ng/mL, divide by 2.496. The figure suggests that levels start to plateau at around 1 month after the beginning of supplementation, reaching a point of saturation after 2-3 months. Without supplementation or sunlight exposure, levels should go down at a comparable rate. The maximum average level shown on the table is 163 nmol/L (65 ng/mL), and refers to a sample of lifeguards.

From the figure we can infer that people on average will plateau at approximately 130 nmol/L, after months of 10,000 IU/d supplementation. That is 52 ng/mL. Assuming a normal distribution with a standard deviation of about 20 percent of the range of average levels, we can expect about 68 percent of those taking that level of supplementation to be in the 42 to 63 ng/mL range.

This might be the range most of us should expect to be in at an intake of 10,000 IU/d. This is the equivalent to the body’s own natural production through sun exposure.

Approximately 32 percent of the population can be expected to be outside this range. A person who is two standard deviations (SDs) above the mean (i.e., average) would be at around 73 ng/mL. Three SDs above the mean would be 83 ng/mL. Two SDs below the mean would be 31 ng/mL.

There are other factors that may affect levels. For example, being overweight tends to reduce them. Excess cortisol production, from stress, may also reduce them.

Supplementing beyond 10,000 IU/d to reach levels much higher than those in the range of 42 to 63 ng/mL may not be optimal. Interestingly, one cannot overdose through sun exposure, and the idea that people do not produce vitamin D3 after 40 years of age is a myth.

One would be taking in about 14,000 IU/d of vitamin D3 by combining sun exposure with a supplemental dose of 4,000 IU/d. Clear signs of toxicity may not occur until one reaches 50,000 IU/d. Still, one may develop other complications, such as kidney stones, at levels significantly above 10,000 IU/d.

Chris Masterjohn has made a different argument, with somewhat similar conclusions. Chris pointed out that there is a point of saturation above which the liver is unable to properly hydroxylate vitamin D3 to produce 25(OH)D.

How likely it is that a person will develop complications like kidney stones at levels above 10,000 IU/d, and what the danger threshold level could be, are hard to guess. Kidney stone incidence is a sensitive measure of possible problems; but it is, by itself, an unreliable measure. The reason is that it is caused by factors that are correlated with high levels of vitamin D, where those levels may not be the problem.

There is some evidence that kidney stones are associated with living in sunny regions. This is not, in my view, due to high levels of vitamin D3 production from sunlight. Kidney stones are also associated with chronic dehydration, and populations living in sunny regions may be at a higher than average risk of chronic dehydration. This is particularly true for sunny regions that are also very hot and/or dry.

Reference

Vieth, R. (1999). Vitamin D supplementation, 25-hydroxyvitamin D concentrations, and safety. American Journal of Clinical Nutrition, 69(5), 842-856.

The China Study II: Wheat flour, rice, and cardiovascular disease

In another post () on the China Study II, I analyzed the effect of total and HDL cholesterol on mortality from all cardiovascular diseases. The main conclusion was that total and HDL cholesterol were protective. Total and HDL cholesterol usually increase with intake of animal foods, and particularly of animal fat. The lowest mortality from all cardiovascular diseases was in the highest total cholesterol range, 172.5 to 180; and the highest mortality in the lowest total cholesterol range, 120 to 127.5. The difference was quite large; the mortality in the lowest range was approximately 3.3 times higher than in the highest.

This post focuses on the intake of two main plant foods, namely wheat flour and rice intake, and their relationships with mortality from all cardiovascular diseases. After many exploratory multivariate analyses, wheat flour and rice emerged as the plant foods with the strongest associations with mortality from all cardiovascular diseases. Moreover, wheat flour and rice have a strong and inverse relationship with each other, which suggests a “consumption divide”. Since the data is from China in the late 1980s, it is likely that consumption of wheat flour is even higher now. As you’ll see, this picture is alarming.

The main model and results

All of the results reported here are from analyses conducted using WarpPLS (). Below is the model with the main results of the analyses. (Click on it to enlarge. Use the "CRTL" and "+" keys to zoom in, and CRTL" and "-" to zoom out.) The arrows explore associations between variables, which are shown within ovals. The meaning of each variable is the following: SexM1F2 = sex, with 1 assigned to males and 2 to females; MVASC = mortality from all cardiovascular diseases (ages 35-69); TKCAL = total calorie intake per day; WHTFLOUR = wheat flour intake (g/day); and RICE = and rice intake (g/day).

The variables to the left of MVASC are the main predictors of interest in the model. The one to the right is a control variable – SexM1F2. The path coefficients (indicated as beta coefficients) reflect the strength of the relationships. A negative beta means that the relationship is negative; i.e., an increase in a variable is associated with a decrease in the variable that it points to. The P values indicate the statistical significance of the relationship; a P lower than 0.05 generally means a significant relationship (95 percent or higher likelihood that the relationship is “real”).

In summary, the model above seems to be telling us that:

- As rice intake increases, wheat flour intake decreases significantly (beta=-0.84; P<0.01). This relationship would be the same if the arrow pointed in the opposite direction. It suggests that there is a sharp divide between rice-consuming and wheat flour-consuming regions.

- As wheat flour intake increases, mortality from all cardiovascular diseases increases significantly (beta=0.32; P<0.01). This is after controlling for the effects of rice and total calorie intake. That is, wheat flour seems to have some inherent properties that make it bad for one’s health, even if one doesn’t consume that many calories.

- As rice intake increases, mortality from all cardiovascular diseases decreases significantly (beta=-0.24; P<0.01). This is after controlling for the effects of wheat flour and total calorie intake. That is, this effect is not entirely due to rice being consumed in place of wheat flour. Still, as you’ll see later in this post, this relationship is nonlinear. Excessive rice intake does not seem to be very good for one’s health either.

- Increases in wheat flour and rice intake are significantly associated with increases in total calorie intake (betas=0.25, 0.33; P<0.01). This may be due to wheat flour and rice intake: (a) being themselves, in terms of their own caloric content, main contributors to the total calorie intake; or (b) causing an increase in calorie intake from other sources. The former is more likely, given the effect below.

- The effect of total calorie intake on mortality from all cardiovascular diseases is insignificant when we control for the effects of rice and wheat flour intakes (beta=0.08; P=0.35). This suggests that neither wheat flour nor rice exerts an effect on mortality from all cardiovascular diseases by increasing total calorie intake from other food sources.

- Being female is significantly associated with a reduction in mortality from all cardiovascular diseases (beta=-0.24; P=0.01). This is to be expected. In other words, men are women with a few design flaws, so to speak. (This situation reverses itself a bit after menopause.)

Wheat flour displaces rice

The graph below shows the shape of the association between wheat flour intake (WHTFLOUR) and rice intake (RICE). The values are provided in standardized format; e.g., 0 is the mean (a.k.a. average), 1 is one standard deviation above the mean, and so on. The curve is the best-fitting U curve obtained by the software. It actually has the shape of an exponential decay curve, which can be seen as a section of a U curve. This suggests that wheat flour consumption has strongly displaced rice consumption in several regions in China, and also that wherever rice consumption is high wheat flour consumption tends to be low.

As wheat flour intake goes up, so does cardiovascular disease mortality

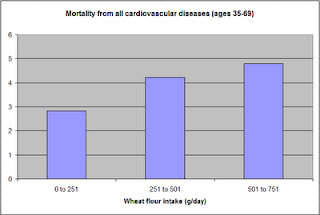
The graphs below show the shapes of the association between wheat flour intake (WHTFLOUR) and mortality from all cardiovascular diseases (MVASC). In the first graph, the values are provided in standardized format; e.g., 0 is the mean (or average), 1 is one standard deviation above the mean, and so on. In the second graph, the values are provided in unstandardized format and organized in terciles (each of three equal intervals).

The curve in the first graph is the best-fitting U curve obtained by the software. It is a quasi-linear relationship. The higher the consumption of wheat flour in a county, the higher seems to be the mortality from all cardiovascular diseases. The second graph suggests that mortality in the third tercile, which represents a consumption of wheat flour of 501 to 751 g/day (a lot!), is 69 percent higher than mortality in the first tercile (0 to 251 g/day).

Rice seems to be protective, as long as intake is not too high

The graphs below show the shapes of the association between rice intake (RICE) and mortality from all cardiovascular diseases (MVASC). In the first graph, the values are provided in standardized format. In the second graph, the values are provided in unstandardized format and organized in terciles.

Here the relationship is more complex. The lowest mortality is clearly in the second tercile (206 to 412 g/day). There is a lot of variation in the first tercile, as suggested by the first graph with the U curve. (Remember, as rice intake goes down, wheat flour intake tends to go up.) The U curve here looks similar to the exponential decay curve shown earlier in the post, for the relationship between rice and wheat flour intake.

In fact, the shape of the association between rice intake and mortality from all cardiovascular diseases looks a bit like an “echo” of the shape of the relationship between rice and wheat flour intake. Here is what is creepy. This echo looks somewhat like the first curve (between rice and wheat flour intake), but with wheat flour intake replaced by “death” (i.e., mortality from all cardiovascular diseases).

What does this all mean?

- Wheat flour displacing rice does not look like a good thing. Wheat flour intake seems to have strongly displaced rice intake in the counties where it is heavily consumed. Generally speaking, that does not seem to have been a good thing. It looks like this is generally associated with increased mortality from all cardiovascular diseases.

- High glycemic index food consumption does not seem to be the problem here. Wheat flour and rice have very similar glycemic indices (but generally not glycemic loads; see below). Both lead to blood glucose and insulin spikes. Yet, rice consumption seems protective when it is not excessive. This is true in part (but not entirely) because it largely displaces wheat flour. Moreover, neither rice nor wheat flour consumption seems to be significantly associated with cardiovascular disease via an increase in total calorie consumption. This is a bit of a blow to the theory that high glycemic carbohydrates necessarily cause obesity, diabetes, and eventually cardiovascular disease.

- The problem with wheat flour is … hard to pinpoint, based on the results summarized here. Maybe it is the fact that it is an ultra-refined carbohydrate-rich food; less refined forms of wheat could be healthier. In fact, the glycemic loads of less refined carbohydrate-rich foods tend to be much lower than those of more refined ones (). (Also, boiled brown rice has a glycemic load that is about three times lower than that of whole wheat bread; whereas the glycemic indices are about the same.) Maybe the problem is wheat flour's  gluten content. Maybe it is a combination of various factors (), including these.

Notes

- The path coefficients (indicated as beta coefficients) reflect the strength of the relationships; they are a bit like standard univariate (or Pearson) correlation coefficients, except that they take into consideration multivariate relationships (they control for competing effects on each variable). Whenever nonlinear relationships were modeled, the path coefficients were automatically corrected by the software to account for nonlinearity.

- The software used here identifies non-cyclical and mono-cyclical relationships such as logarithmic, exponential, and hyperbolic decay relationships. Once a relationship is identified, data values are corrected and coefficients calculated. This is not the same as log-transforming data prior to analysis, which is widely used but only works if the underlying relationship is logarithmic. Otherwise, log-transforming data may distort the relationship even more than assuming that it is linear, which is what is done by most statistical software tools.

- The R-squared values reflect the percentage of explained variance for certain variables; the higher they are, the better the model fit with the data. In complex and multi-factorial phenomena such as health-related phenomena, many would consider an R-squared of 0.20 as acceptable. Still, such an R-squared would mean that 80 percent of the variance for a particularly variable is unexplained by the data.

- The P values have been calculated using a nonparametric technique, a form of resampling called jackknifing, which does not require the assumption that the data is normally distributed to be met. This and other related techniques also tend to yield more reliable results for small samples, and samples with outliers (as long as the outliers are “good” data, and are not the result of measurement error).

- Only two data points per county were used (for males and females). This increased the sample size of the dataset without artificially reducing variance, which is desirable since the dataset is relatively small. This also allowed for the test of commonsense assumptions (e.g., the protective effects of being female), which is always a good idea in a complex analysis because violation of commonsense assumptions may suggest data collection or analysis error. On the other hand, it required the inclusion of a sex variable as a control variable in the analysis, which is no big deal.

- Since all the data was collected around the same time (late 1980s), this analysis assumes a somewhat static pattern of consumption of rice and wheat flour. In other words, let us assume that variations in consumption of a particular food do lead to variations in mortality. Still, that effect will typically take years to manifest itself. This is a major limitation of this dataset and any related analyses.

- Mortality from schistosomiasis infection (MSCHIST) does not confound the results presented here. Only counties where no deaths from schistosomiasis infection were reported have been included in this analysis. Mortality from all cardiovascular diseases (MVASC) was measured using the variable M059 ALLVASCc (ages 35-69).