Wednesday, December 28, 2016
Tooth decay and silver diamine fluoride
Silver diamine fluoride (SDF) is a substance that can be applied on dental caries - where tooth mass has been destroyed by the action of bacteria that feed primarily on simple sugars. (Candy and sugary drinks are major culprits in this respect; fruits are not, in part because of the combination of a relatively low sugar content with the protective effect of the extra chewing needed.) Many studies have shown the effectiveness of SDF in the treatment of dental caries. The chart below is based on a study by Chu and colleagues ().
The chart above compares, in terms of normalized performance, “arrested” caries in a group of children using SDF against a control group not using SDF. Arrested caries are those in which there is no progression of the lesion; that is, in arrested caries the destruction of tooth mass is either stopped or reversed. The control group level can be seen as one in which a limited amount of arrest occurs (probably due to dietary changes and improved dental care), because the percentage of arrests among those treated with SDF was 100! And, yes, in spite of what most dentists will tell you, tooth decay can be reversed ().
As a side note, dentists do not necessarily tell their clients that tooth decay is irreversible because they want to keep the revenue flow coming into their offices. The sad reality is that most dental care patients will not be able to change their diet enough to reverse tooth decay. Because of that, it would arguably be professionally irresponsible to tell those patients that tooth decay progression can be stopped or reversed without treatment. As Weston Price has shown in his pioneering field studies (), reversing tooth decay requires not only elimination of refined sugars but also increased intake of fat-soluble vitamins (particularly vitamins A, D, and K2).
The chart below is from the same study by Chu and colleagues. It compares, also in terms of normalized performance, new caries formed over a period of time in a group of children using SDF against a control group not using SDF. As you can see from this and the previous chart, not only does SDF application stop or reverse tooth decay, it also prevents new dental caries from forming. From the empirical results it appears that this extends to teeth other than the teeth treated with SDF, presumably because of the action of the offending bacteria on the teeth that are next to those with caries.
SDF has been used in the past in various countries such as China, Japan, and New Zealand. Only recently the use of SDF has been approved in the USA. So, next time you go to the dentist to have dental caries treated, ask if they are able to use SDF and what the likely outcomes will be. Probably there will be no injections, drillings, or fillings. It seems that the only downside is that the brown spots characteristic of tooth decay tend to turn black after SDF is successfully used!
Thursday, October 20, 2016
Virtual Paleo Summit video: What is your ideal weight?
You may want to check out my recent video at the (Virtual Paleo Summit) explaining the waist-to-weight ratio theory for estimation of one's ideal weight. The theory is also discussed below. It may look a little complex, but its application is very simple.
***
There is a significant amount of empirical evidence suggesting that, for a given individual and under normal circumstances, the optimal weight is the one that maximizes the ratio below, where: L = lean body mass, and T = total mass.
L / T
L is difficult and often costly to measure. T can be measured easily, as one’s total weight.
Through some simple algebraic manipulations, you can see below that the ratio above can be rewritten in terms of one’s body fat mass (F).
L / T = (T – F) / T = 1 – F / T
Therefore, in order to maximize L / T, one should maximize 1 – F / T. This essentially means that one should minimize the second term, or the ratio below, which is one’s body fat mass (F) divided by one’s weight (T).
F / T
So, you may say, all I have to do is to minimize my body fat percentage. The problem with this is that body fat percentage is very difficult to measure with precision, and, perhaps more importantly, body fat percentage is associated with lean body mass (and also weight) in a nonlinear way.
In English, it becomes increasingly difficult to retain lean body mass as one's body fat percentage goes down. Mathematically, body fat percentage (F / T) is a nonlinear function of T, where this function has the shape of a J curve.
This is what complicates matters, making the issue somewhat counterintuitive. Six-pack abs may look good, but many people would have to sacrifice too much lean body mass for their own good to get there. Genetics definitely plays a role here, as well as other factors such as age.
Keep in mind that this (i.e., F / T) is a ratio, not an absolute measure. Given this, and to facilitate measurement, we can replace F with a variable that is highly correlated with it, and that captures one or more important dimensions particularly well. This new variable would be a proxy for F. One the most widely used proxies in this type of context is waist circumference. We’ll refer to it as W.
W may well be a very good proxy, because it is a measure that is particularly sensitive to visceral body fat mass, an important dimension of body fat mass. W likely captures variations in visceral body fat mass at the levels where this type of body fat accumulation seems to cause health problems.
Therefore, the ratio that most of us would probably want to minimize is the following, where W is one’s waist circumference, and T is one’s weight.
W / T = waist / weight
Based on the experience of HCE () users, variations in this ratio are likely to be small and require 4-decimals or more to be captured. If you want to avoid having so many decimals, you can multiply the ratio by 1000. This will have no effect on the use of the ratio to find your optimal weight; it is analogous to multiplying a ratio by 100 to express it as a percentage.
Also based on the experience of HCE users, there are fluctuations that make the ratio look like it is changing direction when it is not actually doing that. Many of these fluctuations may be due to measurement error.
If you are obese, as you lose weight through dieting, the waist / weight ratio should go down, because you will be losing more body fat mass than lean body mass, in proportion to your total body mass.
It would arguably be wise to stop losing weight when the waist / weight ratio starts going up, because at that point you will be losing more lean body mass than body fat mass, in proportion to your total body mass.
One’s lowest waist / weight ratio at a given point in time should vary depending on a number of factors, including: diet, exercise, general lifestyle, and age. This lowest ratio will also be dependent on one’s height and genetic makeup.
Mathematically, this lowest ratio is the ratio at which d(W / T) / dT = 0 and d(d(W / T) / dT) / dT > 0. That is, the first derivative of W / T with respect to T equals zero, and the second derivative is greater than zero.
The lowest waist / weight ratio is unique to each individual, and can go up and down over time (e.g., resistance exercise will push it down). Here I am talking about one's lowest waist / weight ratio at a given point in time, not one's waist / weight ratio at a given point in time.
This optimal waist / weight ratio theory is one of the most compatible with evidence regarding the lowest mortality body mass index (, ). Nevertheless, it is another ratio that gets a lot of attention in the health-related literature. I am talking about the waist / hip ratio (). In this literature, waist circumference is often used alone, not as part of a ratio.
Labels:
BMI,
body fat,
body fat loss,
waist-to-weight ratio
Friday, September 30, 2016
PLS Applications Symposium; 5 - 7 April 2017; Laredo, Texas
PLS Applications Symposium; 5 - 7 April 2017; Laredo, Texas
(Abstract submissions accepted until 10 February 2017)
*** Health researchers ***
The research techniques discussed in this Symposium are finding growing use among health researchers. This is in part due to steady growth in the use of the software WarpPLS (visit: http://warppls.com) among those researchers. For those interested in learning more, a full-day workshop will be conducted (see below).
*** Only abstracts are needed for the submissions ***
The partial least squares (PLS) method has increasingly been used in a variety of fields of research and practice, particularly in the context of PLS-based structural equation modeling (SEM). The focus of this Symposium is on the application of PLS-based methods, from a multidisciplinary perspective. For types of submissions, deadlines, and other details, please visit the Symposium’s web site:
http://plsas.net
*** Workshop on PLS-SEM ***
On 5 April 2017 a full-day workshop on PLS-SEM will be conducted by Dr. Ned Kock, using the software WarpPLS. Dr. Kock is the original developer of this software, which is one of the leading PLS-SEM tools today; used by thousands of researchers from a wide variety of disciplines, and from many different countries. This workshop will be hands-on and interactive, and will have two parts: (a) basic PLS-SEM issues, conducted in the morning (9 am - 12 noon); and (b) intermediate and advanced PLS-SEM issues, conducted in the afternoon (2 pm - 5 pm). Participants may attend either one, or both of the two parts.
The following topics, among others, will be covered - Running a Full PLS-SEM Analysis - Conducting a Moderating Effects Analysis - Viewing Moderating Effects via 3D and 2D Graphs - Creating and Using Second Order Latent Variables - Viewing Indirect and Total Effects - Viewing Skewness and Kurtosis of Manifest and Latent Variables - Conducting a Multi-group Analysis with Range Restriction - Viewing Nonlinear Relationships - Conducting a Factor-Based PLS-SEM Analysis - Viewing and Changing Missing Data Imputation Settings - Isolating Mediating Effects - Identifying and Dealing with Outliers - Solving Indicator Problems - Solving Collinearity Problems.
-----------------------------------------------------------
Ned Kock
Symposium Chair
http://plsas.net
Labels:
conference,
PLS Applications Symposium,
training,
warppls
Sunday, September 25, 2016
Niacin turbocharges the growth hormone response to anaerobic exercise: A delayed effect
Niacin is also known as vitamin B3, or nicotinic acid. It is an essential vitamin whose deficiency leads to pellagra. In large doses of 1 to 3 g per day it has several effects on blood lipids, including an increase in HDL cholesterol and a marked decreased in fasting triglycerides. Niacin is also a powerful antioxidant.
Among niacin’s other effects, when taken in large doses of 1 to 3 g per day, is an acute elevation in growth hormone secretion. This is a delayed effect, frequently occurring 3 to 5 hours after taking niacin. This effect is independent of exercise.
It is important to note that large doses of 1 to 3 g of niacin are completely unnatural, and cannot be achieved by eating foods rich in niacin. For example, one would have to eat a toxic amount of beef liver (e.g., 15 lbs) to get even close to 1 g of niacin. Beef liver is one of the richest natural sources of niacin.
Unless we find out something completely unexpected about the diet of our Paleolithic ancestors in the future, we can safely assume that they never benefited from the niacin effects discussed in this post.
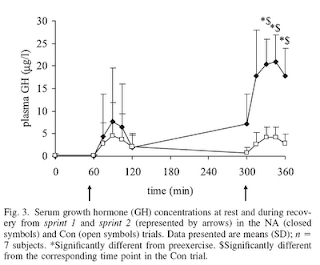
With that caveat, let us look at yet another study on niacin and its effect on growth hormone. Stokes and colleagues (2008) conducted a study suggesting that, in addition to the above mentioned beneficial effects of niacin, there is another exercise-induced effect: niacin “turbocharges” the growth hormone response to anaerobic exercise. The full reference to the study is at the end of this post. Figure 3, shown below, illustrates the effect and its magnitude. Click on it to enlarge.
The closed diamond symbols represent the treatment group. In it, participants ingested a total of 2 g of niacin in three doses: 1 g ingested at 0 min, 0.5 g at 120 min, and 0.5 g at 240 min. The control group ingested no niacin, and is represented by the open square symbols. (The researchers did not use a placebo in the control group; they justified this decision by noting that the niacin flush nullified the benefits of using a placebo.) The arrows indicate points at which all-out 30-second cycle ergometer sprints occurred.
Ignore the lines showing the serum growth hormone levels in between 120 and 300 min; they were not measured within that period.
As you can see, the peak growth hormone response to the first sprint was almost two times higher in the niacin group. In the second sprint, at 300 min, the rise in growth hormone is about 5 times higher in the niacin group.
We know that growth hormone secretion may rise 300 percent with exercise, without niacin. According to this study, this effect may be “turbocharged” up to a 600 percent rise with niacin within 300 min (5 h) of taking it, and possibly 1,500 percent soon after 300 min passed since taking niacin.
That is, not only does niacin boost growth hormone secretion anytime after it is taken, but one still gets the major niacin increase in growth hormone at around 300 min of taking it (which is about the same, whether you exercise or not). Its secretion level at this point is, by the way, higher than its highest level typically reached during deep sleep.
Let me emphasize that the peak growth hormone level achieved in the second sprint is about the same you would get without exercise, namely a bit more than 20 micrograms per liter, as long as you took niacin (see Quabbe's articles at the end of this post).
Still, if you time your exercise session to about 300 min after taking niacin you may have some extra benefits, because getting that peak growth hormone secretion at the time you are exercising may help boost some of the benefits of exercise.
For example, the excess growth hormone secretion may reduce muscle catabolism and increase muscle anabolism, at the same time, leading to an increase in muscle gain. However, there is evidence that growth hormone-induced muscle gain occurs only when testosterone levels are elevated. This explains why growth hormone levels are usually higher in young women than young men, and yet young women do not put on much muscle in response to exercise.
Reference:
Stokes, K.A., Tyler, C., & Gilbert, K.L. (2008). The growth hormone response to repeated bouts of sprint exercise with and without suppression of lipolysis in men. Journal of Applied Physiology, 104(3), 724-728.
Among niacin’s other effects, when taken in large doses of 1 to 3 g per day, is an acute elevation in growth hormone secretion. This is a delayed effect, frequently occurring 3 to 5 hours after taking niacin. This effect is independent of exercise.
It is important to note that large doses of 1 to 3 g of niacin are completely unnatural, and cannot be achieved by eating foods rich in niacin. For example, one would have to eat a toxic amount of beef liver (e.g., 15 lbs) to get even close to 1 g of niacin. Beef liver is one of the richest natural sources of niacin.
Unless we find out something completely unexpected about the diet of our Paleolithic ancestors in the future, we can safely assume that they never benefited from the niacin effects discussed in this post.
With that caveat, let us look at yet another study on niacin and its effect on growth hormone. Stokes and colleagues (2008) conducted a study suggesting that, in addition to the above mentioned beneficial effects of niacin, there is another exercise-induced effect: niacin “turbocharges” the growth hormone response to anaerobic exercise. The full reference to the study is at the end of this post. Figure 3, shown below, illustrates the effect and its magnitude. Click on it to enlarge.
The closed diamond symbols represent the treatment group. In it, participants ingested a total of 2 g of niacin in three doses: 1 g ingested at 0 min, 0.5 g at 120 min, and 0.5 g at 240 min. The control group ingested no niacin, and is represented by the open square symbols. (The researchers did not use a placebo in the control group; they justified this decision by noting that the niacin flush nullified the benefits of using a placebo.) The arrows indicate points at which all-out 30-second cycle ergometer sprints occurred.
Ignore the lines showing the serum growth hormone levels in between 120 and 300 min; they were not measured within that period.
As you can see, the peak growth hormone response to the first sprint was almost two times higher in the niacin group. In the second sprint, at 300 min, the rise in growth hormone is about 5 times higher in the niacin group.
We know that growth hormone secretion may rise 300 percent with exercise, without niacin. According to this study, this effect may be “turbocharged” up to a 600 percent rise with niacin within 300 min (5 h) of taking it, and possibly 1,500 percent soon after 300 min passed since taking niacin.
That is, not only does niacin boost growth hormone secretion anytime after it is taken, but one still gets the major niacin increase in growth hormone at around 300 min of taking it (which is about the same, whether you exercise or not). Its secretion level at this point is, by the way, higher than its highest level typically reached during deep sleep.
Let me emphasize that the peak growth hormone level achieved in the second sprint is about the same you would get without exercise, namely a bit more than 20 micrograms per liter, as long as you took niacin (see Quabbe's articles at the end of this post).
Still, if you time your exercise session to about 300 min after taking niacin you may have some extra benefits, because getting that peak growth hormone secretion at the time you are exercising may help boost some of the benefits of exercise.
For example, the excess growth hormone secretion may reduce muscle catabolism and increase muscle anabolism, at the same time, leading to an increase in muscle gain. However, there is evidence that growth hormone-induced muscle gain occurs only when testosterone levels are elevated. This explains why growth hormone levels are usually higher in young women than young men, and yet young women do not put on much muscle in response to exercise.
Reference:
Stokes, K.A., Tyler, C., & Gilbert, K.L. (2008). The growth hormone response to repeated bouts of sprint exercise with and without suppression of lipolysis in men. Journal of Applied Physiology, 104(3), 724-728.
Labels:
growth hormone,
niacin,
research,
resistance exercise
Friday, August 26, 2016
Growth hormone may rise 300 percent with exercise: Acute increases also occur in cortisol, adrenaline, and noradrenaline
The figure below (click to enlarge) is from the outstanding book Physiology of sport and exercise, by Jack H. Wilmore, David L. Costill, and W. Larry Kenney. If you are serious about endurance or resistance exercise, or want to have a deeper understanding of exercise physiology beyond what one can get in popular exercise books, this book should be in your personal and/or institutional library. It is one of the most comprehensive textbooks on exercise physiology around. The full reference to the book is at the end of this post.
The hormonal and free fatty acid responses shown on the two graphs are to relatively intense exercise combining aerobic and anaerobic components. Something like competitive cross-country running in an area with hills would lead to that type of response. As you can see, cortisol spikes at the beginning, combining forces with adrenaline and noradrenaline (a.k.a. epinephrine and norepinephrine) to quickly increase circulating free fatty acid levels. Then free fatty acid levels are maintained elevated by adrenaline, noradrenaline, and growth hormone. As you can see from the graphs, free fatty acid levels are initially pulled up by cortisol, and then are very strongly correlated with adrenaline and noradrenaline. Those free fatty acids feed muscle, and also lead to the production of ketones, which provide extra fuel for muscle tissue.
Growth hormone stays flat for about 40 minutes, after which it goes up steeply. At around the 90-minute mark, it reaches a level that is quite high; 300 percent higher than it was prior to the exercise session. Natural elevation of circulating growth hormone through intense exercise, intermittent fasting, and restful sleep, leads to a number of health benefits. It helps burn abdominal fat, often hours after the exercise session, and helps build muscle (in conjunction with other hormones, such as testosterone). It appears to increase insulin sensitivity in the long run.
Aerobic activities normally do not elevate growth hormone levels, even though they are healthy, unless they lead to a significant degree of glycogen depletion. Glycogen is stored in the liver and muscle, with muscle storing about 5 times more than the liver (about 500 g in adults). Once those reserves go down significantly during exercise, it seems that growth hormone is recruited to ramp up fat catabolism and facilitate other metabolic processes. Walking for an hour, even if briskly, is good for fat burning, but generates only a small growth hormone elevation. Including a few all-out sprints into that walk can help significantly increase growth hormone secretion.
Having said that, it is not really clear whether growth hormone elevation is a response to glycogen depletion, or whether both happen together in response to another stimulus or related metabolic process. There are other factors that come into play as well. For example, circulating growth hormone increase is moderated by sex hormone (e.g., testosterone, estrogen) secretion, thus larger growth hormone increases in response to exercise are observed in older men than in older women. (Testosterone declines more slowly with age in men than estrogen does in women.) Also, growth hormone increase seems to be correlated with an increase in circulating ketones.
Heavy resistance exercise seems to lead to a higher growth hormone elevation per unit of time than endurance exercise. That is, an intense resistance training session lasting only 30 minutes can lead to an acute circulating growth hormone response, similar to that shown on the figure. The key seems to be reaching the point during the exercise where muscle glycogen stores are significantly depleted. Many people who weight-train achieve this regularly by combining a reasonable number of sets (e.g., 6-12), with repetitions in the muscle hypertrophy range (again, 6-12); and progressive overload, whereby resistance is increased incrementally every session.
Progressive overload is needed because glycogen reserves are themselves increased in response to training, so one has to increase resistance every session to keep up with those increases. This goes on only up to a point, a point of saturation, usually reached by elite athletes. Glycogen is the primary fuel for anaerobic exercise; fat is used as fuel in the recovery period between sets, and after the exercise is over. Glycogen is expended proportionally to the number of calories used in the anaerobic effort. Calories are expended proportionally to the total amount of weight moved around, and are also a function of the movements performed (moving a certain weight 1 feet spends less energy than moving it 3 feet). By the way, not much glycogen is depleted in a 30-minute session. The total caloric expenditure will probably be around 250 calories above the basal metabolic rate, which will require about 63 g of glycogen.
Many sensations are associated with reaching the glycogen depletion level required for an acute growth hormone response during heavy anaerobic exercise. Often light to severe nausea is experienced. Many people report a “funny” feeling, which is unmistakable to them, but very difficult to describe. In some people the “funny” feeling is followed, after even more exertion, by a progressively strong sensation of “pins and needles”, which, unlike that associated with a heart attack, comes slowly and also goes away slowly with rest. Some people feel lightheaded as well.
It seems that the optimal point is reached immediately before the above sensations become bothersome; perhaps at the onset of the “funny” feeling. My personal impression is that the level at which one experiences the “pins and needles” sensation should be avoided, because that is a point where your body is about to “force” you to stop exercising. (Note: I am not a bodybuilder; see “Interesting links” for more extensive resources on the subject.) Besides, go to that point or beyond and significant muscle catabolism may occur, because the body prioritizes glycogen reserves over muscle protein. It will break that protein down to produce glucose via gluconeogenesis to feed muscle glycogenesis.
That the body prioritizes muscle glycogen reserves over muscle protein is surprising to many, but makes evolutionary sense. In our evolutionary past, there were no selection pressures on humans to win bodybuilding tournaments. For our hominid ancestors, it was more important to have the glycogen tank at least half-full than to have some extra muscle protein. Without glycogen, the violent muscle contractions needed for a “fight or flight” response to an animal attack simply cannot happen. And large predators (e.g., a bear) would not feel intimated by big human muscles alone; it would be the human’s response using those muscles that would result in survival or death.
Overall, selection pressures probably favored functional strength combined with endurance, leading to body types similar to those of the hunter-gatherers shown on this post.
Even though the growth hormone response to exercise can be steep, the highest natural growth hormone spike seems to be the one that occurs at night, during deep sleep.
Exercising hard pays off, but only if one sleeps well.
The hormonal and free fatty acid responses shown on the two graphs are to relatively intense exercise combining aerobic and anaerobic components. Something like competitive cross-country running in an area with hills would lead to that type of response. As you can see, cortisol spikes at the beginning, combining forces with adrenaline and noradrenaline (a.k.a. epinephrine and norepinephrine) to quickly increase circulating free fatty acid levels. Then free fatty acid levels are maintained elevated by adrenaline, noradrenaline, and growth hormone. As you can see from the graphs, free fatty acid levels are initially pulled up by cortisol, and then are very strongly correlated with adrenaline and noradrenaline. Those free fatty acids feed muscle, and also lead to the production of ketones, which provide extra fuel for muscle tissue.
Growth hormone stays flat for about 40 minutes, after which it goes up steeply. At around the 90-minute mark, it reaches a level that is quite high; 300 percent higher than it was prior to the exercise session. Natural elevation of circulating growth hormone through intense exercise, intermittent fasting, and restful sleep, leads to a number of health benefits. It helps burn abdominal fat, often hours after the exercise session, and helps build muscle (in conjunction with other hormones, such as testosterone). It appears to increase insulin sensitivity in the long run.
Aerobic activities normally do not elevate growth hormone levels, even though they are healthy, unless they lead to a significant degree of glycogen depletion. Glycogen is stored in the liver and muscle, with muscle storing about 5 times more than the liver (about 500 g in adults). Once those reserves go down significantly during exercise, it seems that growth hormone is recruited to ramp up fat catabolism and facilitate other metabolic processes. Walking for an hour, even if briskly, is good for fat burning, but generates only a small growth hormone elevation. Including a few all-out sprints into that walk can help significantly increase growth hormone secretion.
Having said that, it is not really clear whether growth hormone elevation is a response to glycogen depletion, or whether both happen together in response to another stimulus or related metabolic process. There are other factors that come into play as well. For example, circulating growth hormone increase is moderated by sex hormone (e.g., testosterone, estrogen) secretion, thus larger growth hormone increases in response to exercise are observed in older men than in older women. (Testosterone declines more slowly with age in men than estrogen does in women.) Also, growth hormone increase seems to be correlated with an increase in circulating ketones.
Heavy resistance exercise seems to lead to a higher growth hormone elevation per unit of time than endurance exercise. That is, an intense resistance training session lasting only 30 minutes can lead to an acute circulating growth hormone response, similar to that shown on the figure. The key seems to be reaching the point during the exercise where muscle glycogen stores are significantly depleted. Many people who weight-train achieve this regularly by combining a reasonable number of sets (e.g., 6-12), with repetitions in the muscle hypertrophy range (again, 6-12); and progressive overload, whereby resistance is increased incrementally every session.
Progressive overload is needed because glycogen reserves are themselves increased in response to training, so one has to increase resistance every session to keep up with those increases. This goes on only up to a point, a point of saturation, usually reached by elite athletes. Glycogen is the primary fuel for anaerobic exercise; fat is used as fuel in the recovery period between sets, and after the exercise is over. Glycogen is expended proportionally to the number of calories used in the anaerobic effort. Calories are expended proportionally to the total amount of weight moved around, and are also a function of the movements performed (moving a certain weight 1 feet spends less energy than moving it 3 feet). By the way, not much glycogen is depleted in a 30-minute session. The total caloric expenditure will probably be around 250 calories above the basal metabolic rate, which will require about 63 g of glycogen.
Many sensations are associated with reaching the glycogen depletion level required for an acute growth hormone response during heavy anaerobic exercise. Often light to severe nausea is experienced. Many people report a “funny” feeling, which is unmistakable to them, but very difficult to describe. In some people the “funny” feeling is followed, after even more exertion, by a progressively strong sensation of “pins and needles”, which, unlike that associated with a heart attack, comes slowly and also goes away slowly with rest. Some people feel lightheaded as well.
It seems that the optimal point is reached immediately before the above sensations become bothersome; perhaps at the onset of the “funny” feeling. My personal impression is that the level at which one experiences the “pins and needles” sensation should be avoided, because that is a point where your body is about to “force” you to stop exercising. (Note: I am not a bodybuilder; see “Interesting links” for more extensive resources on the subject.) Besides, go to that point or beyond and significant muscle catabolism may occur, because the body prioritizes glycogen reserves over muscle protein. It will break that protein down to produce glucose via gluconeogenesis to feed muscle glycogenesis.
That the body prioritizes muscle glycogen reserves over muscle protein is surprising to many, but makes evolutionary sense. In our evolutionary past, there were no selection pressures on humans to win bodybuilding tournaments. For our hominid ancestors, it was more important to have the glycogen tank at least half-full than to have some extra muscle protein. Without glycogen, the violent muscle contractions needed for a “fight or flight” response to an animal attack simply cannot happen. And large predators (e.g., a bear) would not feel intimated by big human muscles alone; it would be the human’s response using those muscles that would result in survival or death.
Overall, selection pressures probably favored functional strength combined with endurance, leading to body types similar to those of the hunter-gatherers shown on this post.
Even though the growth hormone response to exercise can be steep, the highest natural growth hormone spike seems to be the one that occurs at night, during deep sleep.
Exercising hard pays off, but only if one sleeps well.
Thursday, July 28, 2016
There are more geniuses among men than among women, and more idiots too
Deary and colleagues (2007) conducted an interesting study on differences in intelligence scores among men and women. In the context of this blog, this study highlights yet one more counterintuitive and intriguing aspect of Darwinian evolution, adding to points previously made in other posts (see here, and here). Evolution may look simple at first glance, but that is a bit of a mirage. In my opinion, to really understand it one has to understand the mathematics underlying it, a lot of which comes from the field of population genetics.
What makes the study by Deary and colleagues (2007) particularly interesting is that its participants were opposite-sex siblings. This helped control for the influence of environmental factors. The downside is that the effect sizes might have been decreased, because of the high gene correlation among siblings, so we could expect larger differences between unrelated groups of men women. The differences, as you will see, are not in overall scores, but in score dispersion.
Let us get straight to the point made by the study. On average, men and women seem to score equally well on intelligence tests. The main difference is that there is more variation in the scores achieved by men than by women, which leads to an interesting effect: there are more geniuses and more idiots among men than among women.
This does NOT mean that a man’s genius is of a higher order; just that there is a tendency for more men to be geniuses (and idiots) than women in any random population sample. The women who are geniuses can be super geniuses, like two-time Nobel Prize winner Marie Curie, the first PERSON to receive such an honor. Albert Einstein is said that have greatly admired her intelligence.
As an illustration of this score dispersion effect, Deary and colleagues (2007) note that: “… for example, in terms of indices of scientific achievement, men were awarded 545 out of the 557 Nobel prizes awarded for science.” On the “idiot” end of the scale: there are a lot more men than women in prison, and one common denominator of prison inmates is that they tend to score very low on intelligence tests. (This is not to say that all criminals have low intelligence; perhaps mostly the ones that get caught do.)
Having said that, it is important to acknowledge that there are multiple types of intelligence, and even multi-indicator intelligence coefficients are usually poor approximations of an overall measure of intelligence (if there is one). This does not invalidate the main point of this post, which is related to score variability.
The table below (from: Deary and colleagues, 2007; click on it to enlarge; full reference at the end of this post) shows scores obtained by men and women (1,292 pairs of opposite-sex siblings) in various subtests of the Armed Services Vocational Aptitude Battery (ASVAB) test.
Note that nearly all of the differences between means (i.e., averages) are significant, but the direction of the differences (captured by the signs of the Cohen’s d coefficients, which are measures of effect size) varies a lot. That is, on several subtests (e.g., “Arithmetic”) men score higher, but in others (e.g., “Numerical operations”) women score higher. It all comes down to men and women scoring equally well overall.
Now look at the columns showing the standard deviations (“SD”) for men and women. In all subtests but two (“Coding speed” and “Numerical operations”) the standard deviation is higher for men; in many cases significantly higher (e.g., 44 percent higher for “Mechanical comprehension”). The standard deviations are about the same for “Coding speed” and “Numerical operations”. What this means is that variability in scores is nearly always higher, often significantly higher, among men than among women. I prepared the schematic figure below to illustrate the effect that this has on the numbers of individuals at the extremes.
The figure above shows two (badly drawn) quasi-normal distributions of scores. (This post shows a better illustration of a normal distribution.) The red curve refers to a distribution with a lower standard deviation than the blue curve; the latter is flatter. Each point on a curve reflects the number of individuals obtaining a particular score, which would be indicated on the horizontal axis. The number of individuals with that score is on the vertical axis. As you can see, the numbers of individuals scoring very high and low (geniuses and idiots, if the scores reflected intelligence) are greater for the blue curve, which is the curve with the higher standard deviation (higher dispersion of scores). The farther one goes to the left or right (the extremes), the bigger this difference becomes.
What does this have to do with evolution?
Well, there are a few possibilities, two of which appear to be particularly compelling. Maybe this effect is due to a combination of these two.
One is that ancestral women, like women today, selected mating partners based on a wide range of traits. Ancestral men on the other hand, like modern men, focused on a much smaller set of traits (Buss, 1995). The end result is more variation in traits, generally speaking, among men than among women. This refers to traits in general, not only intelligence. For example, there seems to be more variation in height among men than among women.
The other possible explanation is that, in our ancestral past, staying out of the extremes of intelligence was associated with higher survival success in both sexes. It seems that the incidence of certain types of mental disease (e.g., schizophrenia) is quite high among geniuses. This leads to more deaths due to related issues – suicide, depression leading to the metabolic syndrome, etc. And this is today, where geniuses can find many opportunities to “shine” in our complex urban societies. In our ancestral past the cognitive demands would have been much lower, and so would the practical value of being a genius.
If staying out of the extremes has indeed enhanced survival success in our evolutionary past, then it is reasonable to expect more women to fit that pattern than men. As with almost any “thing” that enhances survival success, women (especially pre-menopausal) naturally have more of that “thing” than men (e.g., HDL cholesterol).
The reason is that women are more important for the survival of any population than men; today and 1 million years ago. A population of 99 women and 1 man can potentially generate 99 children every few years. Here inbreeding in subsequent generations will be a problem, but that is better than extinction. A population with 99 women and 99 men (or even 1,000 men) will not generate significantly more children.
Reference:
Buss, D.M. (2003). The evolution of desire: Strategies of human mating. New York, NY: Basic Books.
Deary, I.J., Irwing, P., Der, G., & Bates, T.C. (2007). Brother–sister differences in the g factor in intelligence: Analysis of full, opposite-sex siblings from the NLSY1979. Intelligence, 35(5), 451-456.
What makes the study by Deary and colleagues (2007) particularly interesting is that its participants were opposite-sex siblings. This helped control for the influence of environmental factors. The downside is that the effect sizes might have been decreased, because of the high gene correlation among siblings, so we could expect larger differences between unrelated groups of men women. The differences, as you will see, are not in overall scores, but in score dispersion.
Let us get straight to the point made by the study. On average, men and women seem to score equally well on intelligence tests. The main difference is that there is more variation in the scores achieved by men than by women, which leads to an interesting effect: there are more geniuses and more idiots among men than among women.
This does NOT mean that a man’s genius is of a higher order; just that there is a tendency for more men to be geniuses (and idiots) than women in any random population sample. The women who are geniuses can be super geniuses, like two-time Nobel Prize winner Marie Curie, the first PERSON to receive such an honor. Albert Einstein is said that have greatly admired her intelligence.
As an illustration of this score dispersion effect, Deary and colleagues (2007) note that: “… for example, in terms of indices of scientific achievement, men were awarded 545 out of the 557 Nobel prizes awarded for science.” On the “idiot” end of the scale: there are a lot more men than women in prison, and one common denominator of prison inmates is that they tend to score very low on intelligence tests. (This is not to say that all criminals have low intelligence; perhaps mostly the ones that get caught do.)
Having said that, it is important to acknowledge that there are multiple types of intelligence, and even multi-indicator intelligence coefficients are usually poor approximations of an overall measure of intelligence (if there is one). This does not invalidate the main point of this post, which is related to score variability.
The table below (from: Deary and colleagues, 2007; click on it to enlarge; full reference at the end of this post) shows scores obtained by men and women (1,292 pairs of opposite-sex siblings) in various subtests of the Armed Services Vocational Aptitude Battery (ASVAB) test.
Note that nearly all of the differences between means (i.e., averages) are significant, but the direction of the differences (captured by the signs of the Cohen’s d coefficients, which are measures of effect size) varies a lot. That is, on several subtests (e.g., “Arithmetic”) men score higher, but in others (e.g., “Numerical operations”) women score higher. It all comes down to men and women scoring equally well overall.
Now look at the columns showing the standard deviations (“SD”) for men and women. In all subtests but two (“Coding speed” and “Numerical operations”) the standard deviation is higher for men; in many cases significantly higher (e.g., 44 percent higher for “Mechanical comprehension”). The standard deviations are about the same for “Coding speed” and “Numerical operations”. What this means is that variability in scores is nearly always higher, often significantly higher, among men than among women. I prepared the schematic figure below to illustrate the effect that this has on the numbers of individuals at the extremes.
The figure above shows two (badly drawn) quasi-normal distributions of scores. (This post shows a better illustration of a normal distribution.) The red curve refers to a distribution with a lower standard deviation than the blue curve; the latter is flatter. Each point on a curve reflects the number of individuals obtaining a particular score, which would be indicated on the horizontal axis. The number of individuals with that score is on the vertical axis. As you can see, the numbers of individuals scoring very high and low (geniuses and idiots, if the scores reflected intelligence) are greater for the blue curve, which is the curve with the higher standard deviation (higher dispersion of scores). The farther one goes to the left or right (the extremes), the bigger this difference becomes.
What does this have to do with evolution?
Well, there are a few possibilities, two of which appear to be particularly compelling. Maybe this effect is due to a combination of these two.
One is that ancestral women, like women today, selected mating partners based on a wide range of traits. Ancestral men on the other hand, like modern men, focused on a much smaller set of traits (Buss, 1995). The end result is more variation in traits, generally speaking, among men than among women. This refers to traits in general, not only intelligence. For example, there seems to be more variation in height among men than among women.
The other possible explanation is that, in our ancestral past, staying out of the extremes of intelligence was associated with higher survival success in both sexes. It seems that the incidence of certain types of mental disease (e.g., schizophrenia) is quite high among geniuses. This leads to more deaths due to related issues – suicide, depression leading to the metabolic syndrome, etc. And this is today, where geniuses can find many opportunities to “shine” in our complex urban societies. In our ancestral past the cognitive demands would have been much lower, and so would the practical value of being a genius.
If staying out of the extremes has indeed enhanced survival success in our evolutionary past, then it is reasonable to expect more women to fit that pattern than men. As with almost any “thing” that enhances survival success, women (especially pre-menopausal) naturally have more of that “thing” than men (e.g., HDL cholesterol).
The reason is that women are more important for the survival of any population than men; today and 1 million years ago. A population of 99 women and 1 man can potentially generate 99 children every few years. Here inbreeding in subsequent generations will be a problem, but that is better than extinction. A population with 99 women and 99 men (or even 1,000 men) will not generate significantly more children.
Reference:
Buss, D.M. (2003). The evolution of desire: Strategies of human mating. New York, NY: Basic Books.
Deary, I.J., Irwing, P., Der, G., & Bates, T.C. (2007). Brother–sister differences in the g factor in intelligence: Analysis of full, opposite-sex siblings from the NLSY1979. Intelligence, 35(5), 451-456.
Labels:
evolution,
intelligence,
mating,
research,
survival
Saturday, April 23, 2016
The impressive nutrition value of whole dried small fish
When I visited Japan several years ago I noticed a variety of dried small fish for sale in grocery stores and supermarkets. They came in what seemed to be vacuum-packed flat plastic bags, often dried. The packing was a bit like that of beef jerky in the USA. Since I could not read the labels, I could not tell if preservatives or things like sugar were added. Beef jerky often has sugar added to it; at least the popular brands.
I have since incorporated dried or almost dried small fish, eaten whole, into my diet. My family eats it, but they don’t seem to like it as much as I do. The easiest small fish to find for sale where I live are smelts. A previous post has a recipe (). I can easily eat 200 g of smelts, about twice as much as on the plate below; not quite dried, but almost so. The veggies are a mix of lettuce and cabbage.
As you can see from the macronutrient composition below (from Nutritiondata.com, for a 100 g portion), 200 g of smelts have about 112 g of protein, and 36 g of fat. No carbohydrates; or a very small amount of them.
Unless you misguidedly think that they will “give you cholesterol”, the macronutrient to calorie ratio of a plate with 200 g of dried (or almost dried) smelts is very good. Let us take a look at the fat content, below (from Nutritiondata.com as well), which is for 100 g of dried smelts.
The “net” omega-3 content of 200 g of dried smelts, after subtracting the omega-6 content, is approximately 4.4 g. The concept of “net” omega-3 content was discussed in a previous post ().
So, the net omega-3 content of 200 g of dried smelts is the equivalent to the net omega-3 content of about 20 fish oil softgels. (Yes, you read it right!) And you would get a lot more omega-6 from the softgels.
Not to mention the fact that isolated omega-3 and omega-6 fats tend to become oxidized much more easily than when they come in “nature’s package”.
Below is the mineral content (also from Nutritiondata.com) of a 100 g portion. Dried smelts are clearly a very good source of selenium. The significant amount of calcium comes mostly from the bones, as with many varieties of small fish that are eaten whole. Combined with the above, we could say that, overall, the nutrient content is high up there next to beef liver as a super food; a natural multivitamin, if you will.
Smelts, like many small non-predatory fish, are not a significant source of toxic metals. Many people avoid seafood because of concerns about toxic metal contamination, particularly mercury. The infamous incident that led to a major scare in that respect – in Minamata, Japan – did involve consumption of small marine animals. But it also involved years of direct and indirect exposure to very high levels of methylmercury from untreated industrial waste.
Other cases have been reported among populations consuming large amounts of whale, shark, dogfish and other relatively large marine animals with tissues compromised via biomagnification. Generally speaking, large predatory fish and predatory aquatic mammals are best avoided as food. If they are consumed, they should be consumed very sporadically.
Many people would say that a plate like the one above, with smelts and veggies, is not very appetizing. But I can really devour it quickly and go for seconds. How come? I use a special spice that enhances the natural flavor or almost any combination of “natural” foods – foods that are not engineered by humans – making them taste delicious.
This special spice is “hunger”. This spice can be your best friend, or your worst enemy.
I have since incorporated dried or almost dried small fish, eaten whole, into my diet. My family eats it, but they don’t seem to like it as much as I do. The easiest small fish to find for sale where I live are smelts. A previous post has a recipe (). I can easily eat 200 g of smelts, about twice as much as on the plate below; not quite dried, but almost so. The veggies are a mix of lettuce and cabbage.
As you can see from the macronutrient composition below (from Nutritiondata.com, for a 100 g portion), 200 g of smelts have about 112 g of protein, and 36 g of fat. No carbohydrates; or a very small amount of them.
Unless you misguidedly think that they will “give you cholesterol”, the macronutrient to calorie ratio of a plate with 200 g of dried (or almost dried) smelts is very good. Let us take a look at the fat content, below (from Nutritiondata.com as well), which is for 100 g of dried smelts.
The “net” omega-3 content of 200 g of dried smelts, after subtracting the omega-6 content, is approximately 4.4 g. The concept of “net” omega-3 content was discussed in a previous post ().
So, the net omega-3 content of 200 g of dried smelts is the equivalent to the net omega-3 content of about 20 fish oil softgels. (Yes, you read it right!) And you would get a lot more omega-6 from the softgels.
Not to mention the fact that isolated omega-3 and omega-6 fats tend to become oxidized much more easily than when they come in “nature’s package”.
Below is the mineral content (also from Nutritiondata.com) of a 100 g portion. Dried smelts are clearly a very good source of selenium. The significant amount of calcium comes mostly from the bones, as with many varieties of small fish that are eaten whole. Combined with the above, we could say that, overall, the nutrient content is high up there next to beef liver as a super food; a natural multivitamin, if you will.
Smelts, like many small non-predatory fish, are not a significant source of toxic metals. Many people avoid seafood because of concerns about toxic metal contamination, particularly mercury. The infamous incident that led to a major scare in that respect – in Minamata, Japan – did involve consumption of small marine animals. But it also involved years of direct and indirect exposure to very high levels of methylmercury from untreated industrial waste.
Other cases have been reported among populations consuming large amounts of whale, shark, dogfish and other relatively large marine animals with tissues compromised via biomagnification. Generally speaking, large predatory fish and predatory aquatic mammals are best avoided as food. If they are consumed, they should be consumed very sporadically.
Many people would say that a plate like the one above, with smelts and veggies, is not very appetizing. But I can really devour it quickly and go for seconds. How come? I use a special spice that enhances the natural flavor or almost any combination of “natural” foods – foods that are not engineered by humans – making them taste delicious.
This special spice is “hunger”. This spice can be your best friend, or your worst enemy.
Monday, February 29, 2016
Book review: The Eclipse of a Mind
The Eclipse of a Mind () is a 722-page book published in 1942 that describes the life of Alonzo Graves. Alonzo is also listed as the author of the book, even though the narrative is not that of a typical autobiography.
The book is an in-depth study of manic depression. Alonzo is the sufferer. He is a very intelligent college dropout journalist who narrates his lifelong struggle for mental balance. We are taken through World War I, the great Great Depression (iconic photo below: ), the various treatments of bacterial diseases prior to antibiotics, among a variety of other topics; all through Alonzo’s eyes.
This book is rather “dense”, and not very easy to read in a linear fashion – i.e., from beginning to end. Since it is annotated, with comments by various psychiatrists and medical doctors who examined and treated Alonzo, the book is fairly repetitive at points. Nevertheless, it is a fascinating read.
Alonzo delves into important historical events that many today are likely unaware of, such as the Bonus Expeditionary Force movement in the 1930s. World War I veterans had been issued paper money that they could not exchange for real money until 1945. Out-of-work veterans revolted during the Great Depression, demanding early payment. Alonzo was right in the middle of this movement, acting as a journalist and taking the side of the veterans. The ensuing stress caused a manic episode that eventually led to Alonzo's hospitalization.
Manic episodes are characterized by euphoric states and increased levels of activity. The episodes are often triggered by stress. Some people become creative and highly productive during manic states, whereas others become irritable and prone to engaging in risky behavior. Frequently manic episodes are followed by debilitating depression ().
Alonzo’s falls into manic states usually started with benign increases in work-related activity. However, as that high-energy state was maintained for various consecutive days, causing periods of very poor sleep, it often led to psychotic or near-psychotic episodes. This produced a total of five hospitalizations, all of which are described in detail in the book. The book ends with Alonzo moving to Russia, whose government ideology he admired, and never being heard of again.
One of the most interesting aspects of this book is Alonzo’s insights into other people’s mental illnesses, some of whom were manic depressive, combined with his inability to recognize the signs of his own illness. Notably, Alonzo was unable to recognize early signs, or “prodomes” (), which made it difficult for him to avoid entering manic states.
As noted earlier, this book is not an easy read. And it is an old book, copies of which are probably difficult to find today. Nevertheless, it is unique in its tell-it-all style, with detailed narratives from both the patient and doctors about a mental illness that is widespread today. Manic depression is an eminently treatable condition that tends to be highly correlated with creative intelligence ().
A frequently unrecognized reality is put forth by this book. Manic depression is not a “new” condition, even though it may be a “disease of civilization”. The levels of sustained stress found in urban societies are probably much higher than those experienced by our ancestors during most of our evolutionary history, and stress is a trigger of manic depression symptoms. The Eclipse of a Mind is a goldmine of insights into this condition.
Saturday, February 20, 2016
How much dietary protein can you store in muscle? About 15 g/d if you are a gifted bodybuilder
Let us say you are one of the gifted few who are able to put on 1 lb of pure muscle per month, or 12 lbs per year, by combining strength training with a reasonable protein intake. Let us go even further and assume that the 1 lb of muscle that we are talking about is due to muscle protein gain, not glycogen or water. This is very uncommon; one has to really be genetically gifted to achieve that.
And you do that by eating a measly 80 g of protein per day. That is little more than 0.5 g of protein per lb of body weight if you weigh 155 lbs; or 0.4 per lb if you weigh 200 lbs. At the end of the year you are much more muscular. People even think that you’ve been taking steroids; but that just came naturally. The figure below shows what happened with the 80 g of protein you consumed every day. About 15 g became muscle (that is 1 lb divided by 30) … and 65 g “disappeared”!
Is that an amazing feat? Yes, it is an amazing feat of waste, if you think that the primary role of protein is to build muscle. More than 80 percent of the protein consumed was used for something else, notably to keep your metabolic engine running.
A significant proportion of dietary protein also goes into the synthesis of albumin, to which free fatty acids bind in the blood. (Albumin is necessary for the proper use of fat as fuel.) Dietary protein is also used in the synthesis of various body tissues and hormones.
Dietary protein does not normally become body fat, but can be used in place of fat as fuel and thus allow more dietary fat to be stored. It leads to an insulin response, which causes less body fat to be released. In this sense, dietary protein has a fat-sparing effect, preventing it from being used to supply the energy needs of the body.
Nevertheless, the fat-sparing effect of protein is lower than that of another "macronutrient" – alcohol. That is, alcohol takes precedence over protein and carbohydrates for use as fuel. Protein takes precedence over carbohydrates. Neither alcohol nor protein typically becomes body fat. Carbohydrates can become body fat, but only when glycogen stores are full.
What does this mean?
As it turns out, a reasonably high protein intake seems to be quite healthy, and there is nothing wrong with the body using protein to feed its metabolism.
Having said that, one does not need enormous amounts of protein to keep or even build muscle if one is getting enough calories from other sources.
And you do that by eating a measly 80 g of protein per day. That is little more than 0.5 g of protein per lb of body weight if you weigh 155 lbs; or 0.4 per lb if you weigh 200 lbs. At the end of the year you are much more muscular. People even think that you’ve been taking steroids; but that just came naturally. The figure below shows what happened with the 80 g of protein you consumed every day. About 15 g became muscle (that is 1 lb divided by 30) … and 65 g “disappeared”!
Is that an amazing feat? Yes, it is an amazing feat of waste, if you think that the primary role of protein is to build muscle. More than 80 percent of the protein consumed was used for something else, notably to keep your metabolic engine running.
A significant proportion of dietary protein also goes into the synthesis of albumin, to which free fatty acids bind in the blood. (Albumin is necessary for the proper use of fat as fuel.) Dietary protein is also used in the synthesis of various body tissues and hormones.
Dietary protein does not normally become body fat, but can be used in place of fat as fuel and thus allow more dietary fat to be stored. It leads to an insulin response, which causes less body fat to be released. In this sense, dietary protein has a fat-sparing effect, preventing it from being used to supply the energy needs of the body.
Nevertheless, the fat-sparing effect of protein is lower than that of another "macronutrient" – alcohol. That is, alcohol takes precedence over protein and carbohydrates for use as fuel. Protein takes precedence over carbohydrates. Neither alcohol nor protein typically becomes body fat. Carbohydrates can become body fat, but only when glycogen stores are full.
What does this mean?
As it turns out, a reasonably high protein intake seems to be quite healthy, and there is nothing wrong with the body using protein to feed its metabolism.
Having said that, one does not need enormous amounts of protein to keep or even build muscle if one is getting enough calories from other sources.
Labels:
albumin,
alcohol,
carbohydrates,
free fatty acid,
glycogen depletion,
protein
Tuesday, January 26, 2016
Wheat flour, rice and vascular diseases in the China Study II data: Article on Cliodynamics
My article on volume 6, number 2, of the journal Cliodynamics has recently been published; it is titled “Wheat flour versus rice consumption and vascular diseases: Evidence from the China Study II data” (). While this is an academic article, I think that the main body of the article is fairly easy to read. More technical readers may want to check under “Supporting material”, which is one of the links on the left, where they will find a detailed description of the data used and the results of some specialized statistical tests.
In the past I have discussed in this blog the associations with vascular diseases, in the China Study dataset, of wheat flour and rice consumption. The interest in the possible effects of wheat flour AND rice consumption comes from the fact that these foods are similar in some important respects – e.g., they tend to raise insulin levels in similar ways. But as you will see in the article, their associations with vascular diseases are clearly different, particularly when we conduct nonlinear analyses.
While I do not think that wheat flour consumption per se is particularly healthy, the results of the analysis go somewhat against the idea that wheat flour intake is the primary culprit with respect to vascular diseases. The results also go somewhat against the “insulin theory of obesity”, at least in a narrow sense, and call for a broader explanation that includes cultural elements. These points are further elaborated in the article. There is speculation in the article, and also a discussion of possible limitations.
Enjoy!
Labels:
China Study,
cliodynamics,
culture,
insulin,
rice,
statistics,
wheat
Subscribe to:
Posts (Atom)