Do COVID cases spike in cold weather? A look at effective reproduction rates from October to December 2020

Do COVID cases spike in cold weather? In a previous post () I argued that COVID cases may in fact go down in cold weather, due to compensatory adaptation (). The figure below shows the effective COVID reproduction numbers () in various states in the USA from the middle of October to the middle of December 2020. As you can see, as the weather patterns have become colder from October to December, COVID transmission rates have been generally improving.

While the risk of COVID transmission may go up with cold weather, which tends to lead to an increase in indoor activities and potentially higher transmission, people react in a compensatory way. This feedback loop may lead to results that are unexpected and surprising, as we can see here.

The China Study again: A multivariate analysis suggesting that schistosomiasis rules!

In the comments section of Denise Minger’s post on July 16, 2010, which discusses some of the data from the China Study (as a follow up to a previous post on the same topic), Denise herself posted the data she used in her analysis. This data is from the China Study. So I decided to take a look at that data and do a couple of multivariate analyzes with it using WarpPLS (warppls.com).

First I built a model that explores relationships with the goal of testing the assumption that the consumption of animal protein causes colorectal cancer, via an intermediate effect on total cholesterol. I built the model with various hypothesized associations to explore several relationships simultaneously, including some commonsense ones. Including commonsense relationships is usually a good idea in exploratory multivariate analyses.

The model is shown on the graph below, with the results. (Click on it to enlarge. Use the "CRTL" and "+" keys to zoom in, and CRTL" and "-" to zoom out.) The arrows explore causative associations between variables. The variables are shown within ovals. The meaning of each variable is the following: aprotein = animal protein consumption; pprotein = plant protein consumption; cholest = total cholesterol; crcancer = colorectal cancer.

The path coefficients (indicated as beta coefficients) reflect the strength of the relationships; they are a bit like standard univariate (or Pearson) correlation coefficients, except that they take into consideration multivariate relationships (they control for competing effects on each variable). A negative beta means that the relationship is negative; i.e., an increase in a variable is associated with a decrease in the variable that it points to.

The P values indicate the statistical significance of the relationship; a P lower than 0.05 means a significant relationship (95 percent or higher likelihood that the relationship is real). The R-squared values reflect the percentage of explained variance for certain variables; the higher they are, the better the model fit with the data. Ignore the “(R)1i” below the variable names; it simply means that each of the variables is measured through a single indicator (or a single measure; that is, the variables are not latent variables).

I should note that the P values have been calculated using a nonparametric technique, a form of resampling called jackknifing, which does not require the assumption that the data is normally distributed to be met. This is good, because I checked the data, and it does not look like it is normally distributed. So what does the model above tell us? It tells us that:

- As animal protein consumption increases, colorectal cancer decreases, but not in a statistically significant way (beta=-0.13; P=0.11).

- As animal protein consumption increases, plant protein consumption decreases significantly (beta=-0.19; P<0.01). This is to be expected.

- As plant protein consumption increases, colorectal cancer increases significantly (beta=0.30; P=0.03). This is statistically significant because the P is lower than 0.05.

- As animal protein consumption increases, total cholesterol increases significantly (beta=0.20; P<0.01). No surprise here. And, by the way, the total cholesterol levels in this study are quite low; an overall increase in them would probably be healthy.

- As plant protein consumption increases, total cholesterol decreases significantly (beta=-0.23; P=0.02). No surprise here either, because plant protein consumption is negatively associated with animal protein consumption; and the latter tends to increase total cholesterol.

- As total cholesterol increases, colorectal cancer increases significantly (beta=0.45; P<0.01). Big surprise here!

Why the big surprise with the apparently strong relationship between total cholesterol and colorectal cancer? The reason is that it does not make sense, because animal protein consumption seems to increase total cholesterol (which we know it usually does), and yet animal protein consumption seems to decrease colorectal cancer.

When something like this happens in a multivariate analysis, it usually is due to the model not incorporating a variable that has important relationships with the other variables. In other words, the model is incomplete, hence the nonsensical results. As I said before in a previous post, relationships among variables that are implied by coefficients of association must also make sense.

Now, Denise pointed out that the missing variable here possibly is schistosomiasis infection. The dataset that she provided included that variable, even though there were some missing values (about 28 percent of the data for that variable was missing), so I added it to the model in a way that seems to make sense. The new model is shown on the graph below. In the model, schisto = schistosomiasis infection.

So what does this new, and more complete, model tell us? It tells us some of the things that the previous model told us, but a few new things, which make a lot more sense. Note that this model fits the data much better than the previous one, particularly regarding the overall effect on colorectal cancer, which is indicated by the high R-squared value for that variable (R-squared=0.73). Most notably, this new model tells us that:

- As schistosomiasis infection increases, colorectal cancer increases significantly (beta=0.83; P<0.01). This is a MUCH STRONGER relationship than the previous one between total cholesterol and colorectal cancer; even though some data on schistosomiasis infection for a few counties is missing (the relationship might have been even stronger with a complete dataset). And this strong relationship makes sense, because schistosomiasis infection is indeed associated with increased cancer rates. More information on schistosomiasis infections can be found here.

- Schistosomiasis infection has no significant relationship with these variables: animal protein consumption, plant protein consumption, or total cholesterol. This makes sense, as the infection is caused by a worm that is not normally present in plant or animal food, and the infection itself is not specifically associated with abnormalities that would lead one to expect major increases in total cholesterol.

- Animal protein consumption has no significant relationship with colorectal cancer. The beta here is very low, and negative (beta=-0.03).

- Plant protein consumption has no significant relationship with colorectal cancer. The beta for this association is positive and nontrivial (beta=0.15), but the P value is too high (P=0.20) for us to discard chance within the context of this dataset. A more targeted dataset, with data on specific plant foods (e.g., wheat-based foods), could yield different results – maybe more significant associations, maybe less significant.

Below is the plot showing the relationship between schistosomiasis infection and colorectal cancer. The values are standardized, which means that the zero on the horizontal axis is the mean of the schistosomiasis infection numbers in the dataset. The shape of the plot is the same as the one with the unstandardized data. As you can see, the data points are very close to a line, which suggests a very strong linear association.

So, in summary, this multivariate analysis vindicates pretty much everything that Denise said in her July 16, 2010 post. It even supports Denise’s warning about jumping to conclusions too early regarding the possible relationship between wheat consumption and colorectal cancer (previously highlighted by a univariate analysis). Not that those conclusions are wrong; they may well be correct.

This multivariate analysis also supports Dr. Campbell’s assertion about the quality of the China Study data. The data that I analyzed was already grouped by county, so the sample size (65 cases) was not so high as to cast doubt on P values. (Having said that, small samples create problems of their own, such as low statistical power and an increase in the likelihood of error-induced bias.) The results summarized in this post also make sense in light of past empirical research.

It is very good data; data that needs to be properly analyzed!

Does protein leach calcium from the bones? Yes, but only if it is plant protein

The idea that protein leaches calcium from the bones has been around for a while. It is related to the notion that protein, especially from animal foods, increases blood acidity. The body then uses its main reservoir of calcium, the bones, to reduce blood acidity. This post generally supports the opposite view, and adds a twist to it, related to plant protein consumption.

The “eat-meat-lose-bone” idea has apparently become popular due to the position taken by Loren Cordain on the topic. Dr. Cordain has also made several important and invaluable contributions to our understanding of the diets of our Paleolithic ancestors. He has argued in his book, The Paleo Diet, and elsewhere that to counter the acid load of protein one should eat fruits and vegetables. The latter are believed to have an alkaline load.

If the idea that protein leaches calcium from the bones is correct, one would expect to see a negative association between protein consumption and bone mineral density (BMD). This negative association should be particularly strong in people aged 50 and older, who are more vulnerable to BMD losses.

As it turns out, this idea appears to be correct only for plant protein. Animal protein seems to be associated with an increase in BMD, at least according to a widely cited study by Promislow et al. (2002). The study shows that there is a positive multivariate association between animal protein consumption and BMD; an association that becomes negative when plant protein consumption is considered.

The study focused on 572 women and 388 men aged 55–92 years living in Rancho Bernardo, California. Food frequency questionnaires were administered in the 1988–1992 period, and BMD was measured 4 years later. The bar chart below shows the approximate increases in BMD (in g/cm^2) for each 15 g/d increment in protein intake.

The authors reported increments in BMD for different increments of protein (15 and 5 g/d), so the results above are adjusted somewhat from the original values reported in the article. Keeping that in mind, the increment in BMD for men due to animal protein was not statistically significant (P=0.20). That is the smallest bar on the left.

Does protein leach calcium from the bones? Based on this study, the reasonable answers to this question are yes for plant protein, and no for animal protein. For animal protein, it seems to be quite the opposite.

Even more interesting, calcium intake did not seem to be much of a factor. BMD gains due to animal protein seemed to converge to similar values whether calcium intake was high, medium or low. The convergence occurred as animal protein intake increased, and the point of convergence was between 85-90 g/d of animal protein intake.

And high calcium intakes did not seem to protect those whose plant protein consumption was high.

The authors do not discuss specific foods, but one can guess the main plant protein that those folks likely consumed. It was likely gluten from wheat products.

Are the associations above due to: (a) the folks eating animal protein consuming more fruits and vegetables than the folks eating plant protein; or (b) something inherent to animal foods that stimulates an increase in the absorption of dietary calcium, even in small amounts?

This question cannot be answered based on this study; it should have controlled for fruit and vegetable consumption for that.

But if I were to bet, I would bet on (b).

Reference

Promislow, J.H.E., Goodman-Gruen, D., Slymen, D.J., & Barrett-Connor, E. (2002). Protein consumption and bone mineral density in the elderly. American Journal of Epidemiology, 155(7), 636–644.

Do COVID cases spike in cold weather?

Do COVID cases spike in cold weather? To answer this question, it may be instructive to look at COVID figures for Brazil and the US, because these two countries have had similar responses to the pandemic (); and have opposite weather patterns – when it is hot in the US, it is cold in Brazil, and vice-versa. This applies particularly to the most populous areas of the two countries.

At the time of this writing, we had the following approximate numbers for Brazil and the US. Brazil – population: 209.5 million, COVID cases: 4.12 million, and COVID deaths: 126 thousand. US – population: 328.2 million, COVID cases: 6.26 million, and COVID deaths: 188 thousand. The two graphs below show the two following ratios: cases-to-population, and deaths-to-population.

In the last several months since the pandemic hit both countries, it has been generally cold in Brazil and hot in the US. Given this, these ratios are too close to support the assumption that COVID cases spike in cold weather. So, a reasonable answer to the question posed in the title of this post is: probably not.

This brings to mind another question: would indoor activities, such as restaurant dining and movie theater attendance, lead to spikes in COVID cases?

Well, the idea was that cold weather would lead to more indoor activities ...

While risk of infection may go up with cold weather and indoor activities, people react in a compensatory way. This feedback loop may lead to unexpected results.

How can carrying some extra body fat be healthy?

Most of the empirical investigations into the association between body mass index (BMI) and mortality suggest that the lowest-mortality BMI is approximately on the border between the normal and overweight ranges. Or, as Peter put it (): "Getting fat is good."

As much as one may be tempted to explain this based only on the relative contribution of lean body mass to total weight, the evidence suggests that both body fat and lean body mass contribute to this phenomenon. In fact, the evidence suggests that carrying some extra body fat may be healthy for many.

Yet, the scientific evidence strongly suggests that body fat accumulation beyond a certain point is unhealthy. There seems to be a sweet spot of body fat percentage, and that sweet spot may vary a lot across different individuals.

One interesting aspect of most empirical investigations of the association between BMI and mortality is that the participants live in urban or semi-urban societies. When you look at hunter-gatherer societies, the picture seems to be a bit different. The graph below shows the distribution of BMIs among males in Kitava and Sweden, from a study by Lindeberg and colleagues ().



In Sweden, a lowest mortality BMI of 26 would correspond to a point on the x axis that would rise up approximately to the middle of the distribution of data points from Sweden in the graph. It is reasonable to assume that this would also happen in Kitava, in which case the lowest mortality BMI would be around 20.

One of the key differences between urbanites and hunter-gatherers is the greater energy expenditure among the latter; hunter-gatherers generally move more. This provides a clue as to why some extra body fat may be healthy among urbanites. Hunter-gatherers spend more energy, so they have to consume more “natural” food, and thus more nutrients, to maintain their lean body mass.

A person’s energy expenditure is strongly dependent on a few variables, including body weight and physical activity. Let us assume that a hunter-gatherer, due to a reasonably high level of physical activity, maintains a BMI of 20 while consuming 3,000 kilocalories (a.k.a. calories) per day. An urbanite with the same height, but a lower level of physical activity, may need a higher body weight, and thus a higher BMI, to consume 3,000 calories per day at maintenance.

And why would someone want to consume 3,000 calories per day? Why not 1,500? The reason is nutrient intake, particularly micronutrient intake – intake of vitamins and minerals that are used by the body in various processes. Unfortunately it seems that micronutrient supplementation (e.g., a multivitamin pill) is largely ineffective except in cases of pathological deficiency.

Urbanites may need to carry a bit of extra body fat to be able to have an appropriate intake of micronutrients to maintain their lean body structures in a healthy state. Obviously the type of food eaten matters a lot. A high nutrient-to-calorie ratio is generally desirable. However, we cannot forget that we also need to eat fat, in part because without it we cannot properly absorb the all-important fat-soluble vitamins. And dietary fat is the most calorie-dense nutrient of all.

Why not putting on extra muscle instead of carrying the extra fat? For one, that is not easy when you are a sedentary urbanite. Particularly after a certain age, if you try too hard you end up getting injured. But there is another interesting angle to consider. Humans, like many other animals, have genetic “protections” against high muscularity, such as the protein myostatin. Myostatin is produced mostly in muscle cells; it acts on muscle, by inhibiting its growth.

Say what? Why would evolution favor something like myostatin? Big, muscular humans could be at the top of the food chain by physical strength alone; they could kill a lion with their bare hands. Well, it is possible. (Many men like to think of themselves as warriors, probably because most of them are not.) But evolution favors what works best given the ecological niches available. In our case, it favored bigger and more plastic brains to occupy what Steve Pinker called a “cognitive niche”.

Even though fat mass is not inert, secreting a number of hormones into the bloodstream, the micronutrient “need” of fat mass is likely much lower than the micronutrient need of non-fat mass. That is, a kilogram of lean mass likely puts a higher demand on micronutrients than a kilogram of fat mass. This should be particularly the case for organs, such as the liver, but also applies to muscle tissue.

While gaining muscle mass through moderate exercise is extremely healthy, bulking up beyond one’s natural limitations may actually backfire. It could increase the demand for micronutrients above what a person can actually consume and absorb through a healthy nutritious diet. Some extra fat mass allows for a higher level of micronutrient intake at weight maintenance, with a lower demand for micronutrients than the same amount of extra lean mass.

Some people are naturally more muscular. Their frame and underlying organ-based capabilities probably support that. It is often visibly noticeable when they go beyond their organ-based capabilities. A common trait among many professional bodybuilders, who usually go beyond the genetic gifts that they naturally have, is an abnormal swelling of internal organs.

What complicates this discussion is that all of this seems to vary from individual to individual. People have to find their sweet spots, and doing that may not be the simplest of tasks. For example, even measuring body fat percentage with some precision is difficult and costly. Also, certain types of fat are less desirable than others – visceral versus subcutaneous body fat. It is not easy differentiating one from the other ().

How do you find your sweet spot in terms of body fat percentage? One of the most promising approaches is to find the point at which your waist-to-weight ratio is minimized ().

Eating fish whole: Sardines

Different parts of a fish have different types of nutrients that are important for our health; this includes bones and organs. Therefore it makes sense to consume the fish whole, not just filets made from it. This is easier to do with small than big fish.

Small fish have the added advantage that they have very low concentrations of metals, compared to large fish. The reason for this is that small fish are usually low in the food chain, typically feeding mostly on plankton, especially algae. Large carnivorous fish tend to accumulate metals in their body, and their consumption over time may lead to the accumulation of toxic levels of metals in our bodies.

One of my favorite types of small fish is the sardine. The photo below is of a dish of sardines and vegetables that I prepared recently. Another small fish favorite is the smelt (see this post). I buy wild-caught sardines regularly at the supermarket.

Sardines are very affordable, and typically available throughout the year. In fact, sardines usually sell for the lowest price among all fish in my supermarket; lower even than tilapia and catfish. I generally avoid tilapia and catfish because they are often farmed (tilapia, almost always), and have a poor omega-6 to omega-3 ratio. Sardines are rich in omega-3, which they obtain from algae. They have approximately 14 times more omega-3 than omega-6 fatty acids. This is an excellent ratio, enough to make up for the poorer ratio of some other foods consumed on a day.

This link gives a nutritional breakdown of canned sardines; possibly wild, since they are listed as Pacific sardines. (Fish listed as Atlantic are often farm-raised.) The wild sardines that I buy and eat probably have a higher vitamin and mineral content that the ones the link refers to, including higher calcium content, because they are not canned or processed in any way. Two sardines should amount to a little more than 100 g; of which about 1.6 g will be the omega-3 content. This is a pretty good amount of omega-3, second only to a few other fish, like wild-caught salmon.

Below is a simple recipe. I used it to prepare the sardines shown on the photo above.

- Steam cook the sardines for 1 hour.
- Spread the steam cooked sardines on a sheet pan covered with aluminum foil; use light olive oil to prevent the sardines from sticking to the foil.
- Preheat the oven to 350 degrees Fahrenheit.
- Season the steam cooked sardines to taste; I suggest using a small amount of salt, and some chili powder, garlic powder, cayenne pepper, and herbs.
- Bake the sardines for 30 minutes, turn the oven off, and leave them there for 1 hour.

The veggies on the plate are a mix of the following: sweet potato, carrot, celery, zucchini, asparagus, cabbage, and onion. I usually add spinach but I had none around today. They were cooked in a covered frying pan, with olive oil and a little bit of water, in low heat. The cabbage and onion pieces were added to the mix last, so that in the end they had the same consistency as the other veggies.

I do not clean, or gut, my sardines. Normally I just wash them in water, as they come from the supermarket, and immediately start cooking them. Also, I eat them whole, including the head and tail. Since they feed primarily on plant matter, and have a very small digestive tract, there is not much to be “cleaned” off of them anyway. In this sense, they are like smelts and other small fish.

For many years now I have been eating them like that; and so have my family and some friends. Other than some initial ew’s, nobody has ever had even a hint of a digestive problem as a result of eating the sardines like I do. This is very likely the way most of our hominid ancestors ate small fish.

If you prepare the sardines as above, they will be ready to store, or eat somewhat cold. There are several variations of this recipe. For example, you can bake the sardines for 40 minutes, and then serve them hot.

You can also add the stored sardines later to a soup, lightly steam them in a frying pan (with a small amount of water), or sauté them for a meal. For the latter I would recommend using coconut oil and low heat. Butter can also be used, which will give the sardines a slightly different taste.

Ketones and Ketosis: Physiological and pathological forms

Ketones are compounds that have a specific chemical structure. The figure below (from: Wikipedia) shows the chemical structure of various types of ketones. As you can see, all ketones share a carbonyl group; that is the “O=” part of their chemical structure. A carbonyl group is an oxygen atom double-bonded to a carbon atom.

Technically speaking, many substances can be classified as ketones. Not all of these are involved in the same metabolic processes in humans. For example, fructose is technically a ketone, but it is not one of the three main ketones produced by humans from dietary macronutrients (discussed below), and is not metabolized in the same way as are those three main ketones.

Humans, as well as most other vertebrates, produce three main ketones (also known as ketone bodies) from dietary macronutrients. These are acetone, acetoacetate and beta-hydroxybutyrate. Low carbohydrate diets tend to promote glycogen depletion, which in turn leads to increased production of these ketones. Glycogen is stored in the liver and muscles. Liver glycogen is used by the body to maintain blood glucose levels within a narrow range in the fasted state. Examples of diets that tend to promote glycogen depletion are the Atkins Diet and Kwaśniewski’s Optimal Diet.

A search for articles on ketosis in scientific databases usually returns a large number of articles dealing with ketosis in cows. Why? The reason is that ketosis reduces milk production, by both reducing the amount of fat and glucose available for milk synthesis. In fact, ketosis is referred to as a “disease” in cows.

In humans, most articles on ketosis refer to pathological ketosis (a.k.a. ketoacidosis), especially in the context of uncontrolled diabetes. One notable exception is an article by Williamson (2005), from which the table below was taken. The table shows ketone concentrations in the blood under various circumstances, in mmol/l.

As you can see, relatively high concentrations of ketones occur in newborn babies (neonate), in adults post-exercise, and in adults fed a high fat diet. Generally speaking, a high fat diet is a low carbohydrate diet, and a high carbohydrate diet is a low fat diet. (One occasionally sees diets that are high in both carbohydrates and fat; which seem excellent at increasing body fat and thus reducing life span. This diet is apparently popular among sumo wrestlers, where genetics and vigorous exercise usually counter the negative diet effects.)

Situations in which ketosis occurs in newborn babies (neonate), in adults post-exercise, and in adults fed a high fat diet are all examples of physiological, or benign, ketosis. Ketones are also found in low concentrations in adults fed a standard American diet.

Ketones are found in very high concentrations in adults with untreated diabetes. This is an example of pathological ketosis, even though ketones are produced as part of a protective compensatory mechanism to spare glucose for the brain and red blood cells (which need glucose to function properly). Pathological ketosis leads to serum ketone levels that can be as much as 80 times (or more) those found in physiological ketosis.

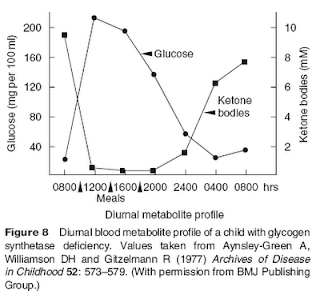
Serum ketone concentrations increase proportionally to decreases in stored glycogen and, when glycogen is low or absent, correlate strongly (and inversely) with blood glucose levels. In some individuals glycogen is practically absent due to a genetic condition that leads to hepatic glycogen synthase deficiency. This is a deficiency of the enzyme that promotes glycogen synthesis by the liver. The figure below (also from Williamson, 2005) shows the variations in glucose and ketone levels in a child with glycogen synthase deficiency.

What happened with this child? Williamson answers this question: “It is of interest that this particular child suffered no ill effects from the daily exposure to high concentrations of ketone bodies, underlining their role as normal substrates for the brain when available.”

Unlike glucose and lipoprotein-bound fats (in VLDL, for example), unused ketones cannot be converted back to substances that can be stored by the body. Thus excess ketones are eliminated in the urine; leading to their detection by various tests, e.g., Ketostix tests. This elimination of unused ketones in the urine is one of the reasons why low carbohydrate diets are believed to lead to enhanced body fat loss.

In summary, ketones are present in the blood most of the time, in most people, whether they are on a ketogenic diet or not. If they do not show up in the urine, it does not mean that they are not present in the blood; although it usually means that their concentration in the blood is not that high. Like glucose, ketones are soluble in water, and thus circulate in the blood without the need for carriers (e.g., albumin, which is needed for the transport of free fatty acids; and VLDL, needed for the transport of triglycerides). Like glucose, they are used as sources of energy by the brain and by muscle tissues.

It has been speculated that ketosis leads to accelerated aging, through the formation of advanced glycation endproducts (AGEs), a speculation that seems to be largely unfounded (see this post). It is difficult to believe that a metabolic process that is universally found in babies and adults post-exercise would have been favored by evolution if it led to accelerated aging.

References:

Williamson, D.H. (2005). Ketosis. Encyclopedia of Human Nutrition, 91-98.

Herd immunity

The figure below is adapted from an article published in 2011 by Fine and colleagues (). The article discusses the concept of “herd immunity”: individuals with immunity against a disease act as a “shield” for the community, slowing or stopping the spread of the disease.

At the top of the figure, the number of infected individuals grows exponentially, until a certain number of individuals with immunity is achieved. At the bottom of the figure, those with immunity “absorb and kill” the infectious agent, without passing it forward – significantly limiting the progression of the disease.

This illustrates the likely impact of vaccination in cases where immunity being acquired through full infection is problematic, such as with COVID-19. In these cases, vaccination would slow or stop the spread of the disease, even if only a proportion of the community is vaccinated.

That is, until the infectious agent mutates!

China’s relaxing of COVID-19 social distancing policy after containment appears to have worked

The graphs below summarize key results from a study published in early 2020 by Ainslie and colleagues (). Dr. Ainslie is in the Faculty of Medicine, School of Public Health, Imperial College London. The study looked at within-city movement, as a proxy for economic activity, and how that movement has influenced the numbers of new cases of COVID-19 in various areas, after initial containment.

As you can see, after initial containment is achieved, within-city movement (measured through a “Movement Index”) seems to be uncorrelated with new COVID-19 cases; or somewhat negatively correlated, as the authors note.

This surprising and counterintuitive outcome may be due to people becoming much more cautious about social interactions.